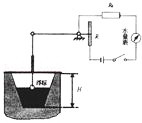
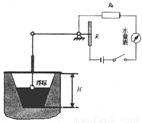
题目内容
 小明同学为邻居王大爷的屋顶水池设计了一个测定水池内水面高度的装置(其原理如图所示),浮标上升(或下降)的高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比.R0=12Ω,电源的电压为6V,水量表由量程适中的电流表充当.池内水深为
小明同学为邻居王大爷的屋顶水池设计了一个测定水池内水面高度的装置(其原理如图所示),浮标上升(或下降)的高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比.R0=12Ω,电源的电压为6V,水量表由量程适中的电流表充当.池内水深为| 1 | 2 |
(1)试证明池中水对池底的压强p与水深h的关系为p=ρgh(式中ρ为水的密度,g为物体所受重力与其质量的比值).
(2)滑动变阻器R的总电阻为多大?
(3)当电流表的示数为多少时表示池中的水已全部流出?
分析:(1)水平上物体的压力和自身的重力相等,根据密度公式和重力公式得出容器内水对容器底的压力,根据p=
表示出容器底受到的压强;
(2)滑片在R的中央时,电路中的电流为0.3A,根据欧姆定律求出总电阻,根据电阻的串联求出滑动变阻器接入电路中的电阻,进一步求出滑动变阻器R的总电阻;
(3)先求出水深从
H到H时阻值变化量,然后根据浮标高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比,即可求出水全部流出时,滑动变阻器接入电路的阻值大小,根据欧姆定律即可求出电流表的示数.
| F |
| S |
(2)滑片在R的中央时,电路中的电流为0.3A,根据欧姆定律求出总电阻,根据电阻的串联求出滑动变阻器接入电路中的电阻,进一步求出滑动变阻器R的总电阻;
(3)先求出水深从
| 1 |
| 2 |
解答:解:(1)容器内作用在容器底部水的质量等于容器底上面水柱的质量,则
m=ρV=ρSh,
对容器底的压力:
F=G=mg=ρShg,
容器底受到的压强:
p=
=
=ρgh;
(2)滑片在R的中央时,R0与R串联,电路中的电流为0.3A,
根据欧姆定律可得,电路中的总电阻:
R总=
=
=20Ω,
∵串联电路中总电阻等于各分电阻之和,
∴滑动变阻器接入电路中的电阻:
=R总-R0=20Ω-12Ω=8Ω,
∴R=16Ω;
(3)当电路中电流为0.4A时,滑动变阻器接入电路的电阻:
R′=
-12Ω=
-12Ω=3Ω,
∵浮标高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比,
∴当浮标从0.5H到H时,滑动变阻器的电阻变化为8Ω-3Ω=5Ω,
∴当池中水全部流出时,浮标从0.5H到0,滑动变阻器的阻值变化仍然为5Ω,
即当池中水全部流出时,滑动变阻器接入电路中的电阻为:
R′=8Ω+5Ω=13Ω,
电流表的示数为:
I′=
=
=0.24A.
答:(1)证明过程如上所示;
(2)滑动变阻器R的总电阻为16Ω;
(3)当电流表的示数为0.24A时表示池中的水已全部流出.
m=ρV=ρSh,
对容器底的压力:
F=G=mg=ρShg,
容器底受到的压强:
p=
| F |
| S |
| ρShg |
| S |
(2)滑片在R的中央时,R0与R串联,电路中的电流为0.3A,
根据欧姆定律可得,电路中的总电阻:
R总=
| U |
| I |
| 6V |
| 0.3A |
∵串联电路中总电阻等于各分电阻之和,
∴滑动变阻器接入电路中的电阻:
| R |
| 2 |
∴R=16Ω;
(3)当电路中电流为0.4A时,滑动变阻器接入电路的电阻:
R′=
| U |
| I′ |
| 6V |
| 0.4A |
∵浮标高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比,
∴当浮标从0.5H到H时,滑动变阻器的电阻变化为8Ω-3Ω=5Ω,
∴当池中水全部流出时,浮标从0.5H到0,滑动变阻器的阻值变化仍然为5Ω,
即当池中水全部流出时,滑动变阻器接入电路中的电阻为:
R′=8Ω+5Ω=13Ω,
电流表的示数为:
I′=
| U |
| R0+R′ |
| 6V |
| 12Ω+13Ω |
答:(1)证明过程如上所示;
(2)滑动变阻器R的总电阻为16Ω;
(3)当电流表的示数为0.24A时表示池中的水已全部流出.
点评:本题考查了液体压强公式的证明和串联电路的特点以及欧姆定律的灵活应用,利用好“浮标高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比”是关键,要注意容器内水对容器底的压力仅仅是指容器底上面水柱的质量,不是容器所以水的质量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
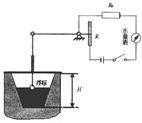 小明同学为邻居王大爷的屋顶水池设计了一个测定水池内水面高度的装置,浮标高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比.R0=12欧,电源电压为6V,水量表由量程适中的电流表充当.池内水深为0.5H时,金属滑片正好在R的中央,如图所示,此时电流表示数为0.3A;池内水深H时,电流表示数为0.4A.①滑动变阻器R的总电阻为多大?②当电流表的示数为多少时表示池中的水已全部流出?
小明同学为邻居王大爷的屋顶水池设计了一个测定水池内水面高度的装置,浮标高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比.R0=12欧,电源电压为6V,水量表由量程适中的电流表充当.池内水深为0.5H时,金属滑片正好在R的中央,如图所示,此时电流表示数为0.3A;池内水深H时,电流表示数为0.4A.①滑动变阻器R的总电阻为多大?②当电流表的示数为多少时表示池中的水已全部流出?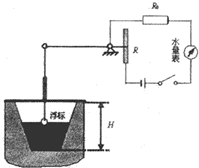 小明同学为邻居王大爷的屋顶水池设计了一个测定水池内水面高度的装置(其原理如图所示),浮标上升(或下降)的高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比.R0=12Ω,电源的电压为6V,水量表由量程适中的电流表充当.池内水深为
小明同学为邻居王大爷的屋顶水池设计了一个测定水池内水面高度的装置(其原理如图所示),浮标上升(或下降)的高度与滑动变阻器R的金属滑片下移(或上移)的距离成正比.R0=12Ω,电源的电压为6V,水量表由量程适中的电流表充当.池内水深为 H时,金属滑片正好在R的中央,如图所示,此时电流表示数为0.3A;水深为H时,电流表示数为0.4A.
H时,金属滑片正好在R的中央,如图所示,此时电流表示数为0.3A;水深为H时,电流表示数为0.4A.