题目内容
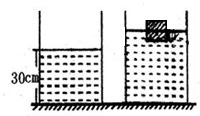 如图所示,一圆柱形容器放在水平桌面上,其底面积为200cm2(容器的厚度忽略不计),内盛30cm深的水.现将质量为0.6kg,边长为10cm的正方体木块放在水中,(g=10N/kg)求:
如图所示,一圆柱形容器放在水平桌面上,其底面积为200cm2(容器的厚度忽略不计),内盛30cm深的水.现将质量为0.6kg,边长为10cm的正方体木块放在水中,(g=10N/kg)求:
(1)木块的密度是多少?
(2)未放木块时,水对容器底的压强是多大?
(3)放木块后,容器对桌面的压强增加了多少?
(4)木块下底面所受水的压强是多少?
解:(1)木块的体积为:
V=(0.1m)3=0.001m3,
根据密度公式可得,木块的密度:
ρ木=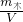 =
=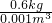 =0.6×103kg/m3;
=0.6×103kg/m3;
(2)未放木块时,水对容器底的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa;
(3)木块的重力为:
G木=m木g=0.6kg×10N/kg=6N,
∵放入木块后水未溢出,
∴容器对桌面的压力增加了△F=G木=6N,
容器对桌面的压强增加了△p= =
= =300Pa;
=300Pa;
(4)∵ρ木<ρ水,
∴木块静止时处于漂浮状态,则F浮=G木=6N,
根据阿基米德原理可得:
V排=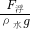 =
= =6×10-4m3,
=6×10-4m3,
木块下底面浸入水中的深度:
h′=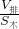 =
= =0.06m,
=0.06m,
木块下底面所受水的压强:
p′=ρ水gh′=1.0×103kg/m3×10N/kg×0.06m=600Pa.
答:(1)木块的密度是0.6×103kg/m3;
(2)未放木块时,水对容器底的压强是3000Pa;
(3)放木块后,容器对桌面的压强增加了300Pa;
(4)木块下底面所受水的压强是600Pa.
分析:(1)先根据正方体木块的边长求出体积,再利用密度公式求木块的密度;
(2)知道水深和水的密度,利用液体压强公式求出未放木块时水对容器底的压强;
(3)知道容器底面积(桌面受力面积)和增大的压力(木块重),利用压强定义式求容器对桌面增加的压强值;
(4)木块的密度小于水的密度,则木块静止时处于漂浮状态,受到的浮力和自身的重力相等,根据阿基米德原理求出排开水的体积,再根据体积公式求出木块下底面浸入水中的深度,最后根据液体压强公式求出木块下底面所受水的压强.
点评:本题综合考查了密度的计算、重力的计算、液体压强的计算、浮力的计算(阿基米德原理)、物体浮沉条件、固体压强的计算,知识点多,综合性强,属于难题;本题的最后一问也可以通过浮力产生的原因进行解答,即先求出底面积,然后求出浮力,最后根据下底面受到的压力减掉上底面受到的压力等于木块受到的浮力求压力.
V=(0.1m)3=0.001m3,
根据密度公式可得,木块的密度:
ρ木=
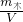 =
=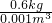 =0.6×103kg/m3;
=0.6×103kg/m3;(2)未放木块时,水对容器底的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa;
(3)木块的重力为:
G木=m木g=0.6kg×10N/kg=6N,
∵放入木块后水未溢出,
∴容器对桌面的压力增加了△F=G木=6N,
容器对桌面的压强增加了△p=
 =
= =300Pa;
=300Pa;(4)∵ρ木<ρ水,
∴木块静止时处于漂浮状态,则F浮=G木=6N,
根据阿基米德原理可得:
V排=
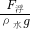 =
= =6×10-4m3,
=6×10-4m3,木块下底面浸入水中的深度:
h′=
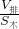 =
= =0.06m,
=0.06m,木块下底面所受水的压强:
p′=ρ水gh′=1.0×103kg/m3×10N/kg×0.06m=600Pa.
答:(1)木块的密度是0.6×103kg/m3;
(2)未放木块时,水对容器底的压强是3000Pa;
(3)放木块后,容器对桌面的压强增加了300Pa;
(4)木块下底面所受水的压强是600Pa.
分析:(1)先根据正方体木块的边长求出体积,再利用密度公式求木块的密度;
(2)知道水深和水的密度,利用液体压强公式求出未放木块时水对容器底的压强;
(3)知道容器底面积(桌面受力面积)和增大的压力(木块重),利用压强定义式求容器对桌面增加的压强值;
(4)木块的密度小于水的密度,则木块静止时处于漂浮状态,受到的浮力和自身的重力相等,根据阿基米德原理求出排开水的体积,再根据体积公式求出木块下底面浸入水中的深度,最后根据液体压强公式求出木块下底面所受水的压强.
点评:本题综合考查了密度的计算、重力的计算、液体压强的计算、浮力的计算(阿基米德原理)、物体浮沉条件、固体压强的计算,知识点多,综合性强,属于难题;本题的最后一问也可以通过浮力产生的原因进行解答,即先求出底面积,然后求出浮力,最后根据下底面受到的压力减掉上底面受到的压力等于木块受到的浮力求压力.

练习册系列答案
相关题目
 (2012?呼和浩特)圆柱形容器底面积是500cm2,高为40cm,盛满水后放在水平放置的接水盘中,现将一质量为7.9kg的实心正方体金属块轻轻地放入圆柱形容器中,静止时如图所示,此时测得溢出的水的体积为1dm3.求:
(2012?呼和浩特)圆柱形容器底面积是500cm2,高为40cm,盛满水后放在水平放置的接水盘中,现将一质量为7.9kg的实心正方体金属块轻轻地放入圆柱形容器中,静止时如图所示,此时测得溢出的水的体积为1dm3.求: 圆柱形容器底面积为500cm2,高为40cm,盛满水后放在水平桌面的中央.现将一质量为7.9kg的实心正方体金属块轻轻放入圆柱形容器中,静止时如图所示.ρ铁=7.9×103kg/m3,g取10N/kg.求:
圆柱形容器底面积为500cm2,高为40cm,盛满水后放在水平桌面的中央.现将一质量为7.9kg的实心正方体金属块轻轻放入圆柱形容器中,静止时如图所示.ρ铁=7.9×103kg/m3,g取10N/kg.求: 如图所示,放在水平桌面上的薄壁圆柱形容器重4N,底面积为100cm2,现将一重为10N的物块浸没水中,容器内水面由16cm上升到20cm.(g取10N/kg,ρ水=1.0×103kg/m3)
如图所示,放在水平桌面上的薄壁圆柱形容器重4N,底面积为100cm2,现将一重为10N的物块浸没水中,容器内水面由16cm上升到20cm.(g取10N/kg,ρ水=1.0×103kg/m3)
