题目内容
 (2000?天津)在一圆柱形容器中盛有水,水面漂浮着一个小容器.当将一个实心小塑料球放入小容器中后,大容器中的水面上升的高度是h1,如图所示.若把这个塑料球从小容器中拿出投入大容器的水中,液面又降低了h2,求这个塑料小球的密度.
(2000?天津)在一圆柱形容器中盛有水,水面漂浮着一个小容器.当将一个实心小塑料球放入小容器中后,大容器中的水面上升的高度是h1,如图所示.若把这个塑料球从小容器中拿出投入大容器的水中,液面又降低了h2,求这个塑料小球的密度.分析:根据题意,利用容器的底面积和水上升的高度表示开小球和小容器排开水的体积;根据漂浮的条件,利用体积、密度和表示出小球的重力与浮力的关系;利用容器的底面积和水面上升的高度表示出小球排开水的体积,分别列出关系式,联立解之即可.
解答:解:设大容器的底面积为S,塑料球体积为V塑,密度为ρ塑,当把塑料球放入小容器中时,排开水的体积为V排,则有:
V排=Sh1---①
V塑ρ塑g=V排ρ水g----②
当把塑料球从小容器中拿出放入水中后,塑料球排开水的体积为V塑,则:
△V=V排-V塑=Sh2-----③
可得,
=
,
化简可得:V排h2=V排h1-V塑h1
V塑h1=(h1-h2)V排----④
可得:ρ塑=
ρ水.
答:这个塑料小球的密度ρ塑=
ρ水.
V排=Sh1---①
V塑ρ塑g=V排ρ水g----②
当把塑料球从小容器中拿出放入水中后,塑料球排开水的体积为V塑,则:
△V=V排-V塑=Sh2-----③
| ① |
| ② |
| V排 |
| V排-V塑 |
| h1 |
| h2 |
化简可得:V排h2=V排h1-V塑h1
V塑h1=(h1-h2)V排----④
| ② |
| ④ |
| h1 |
| h1-h2 |
答:这个塑料小球的密度ρ塑=
| h1 |
| h1-h2 |
点评:本题有一定的难度,考查了学生的综合分析能力.解答本题的关键是对实心球质量和体积的求解,质量需要根据物体的浮沉条件和阿基米德原理进行求解,体积需要根据实心球前后V排的变化和物体的浮沉条件去分析.

练习册系列答案
相关题目
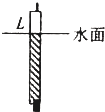 (2000?天津)一只未点燃的蜡烛的下面插入一根小铁钉使蜡烛能直立漂浮在水面上,露出长度为L,如图所示.当把蜡烛水面以上部分截掉后剩余部分( )
(2000?天津)一只未点燃的蜡烛的下面插入一根小铁钉使蜡烛能直立漂浮在水面上,露出长度为L,如图所示.当把蜡烛水面以上部分截掉后剩余部分( )