题目内容
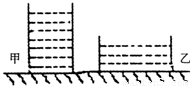
甲、乙两容器中装有质量相等的水，水温分别为25℃和75℃，现将一温度为65℃的金属球放入甲容器中，热平衡后水温升高到45℃，然后迅速取出金属球并放入乙容器中，热平衡后乙容器中水温为（不计热量散失和水的质量的变化）（ ）
分析：（1）首先利用金属球放入25℃的水中时，两者发生热传递，根据两者温度的变化，利用热平衡方程确定水的质量与比热容的乘积和金属球的质量与比热容的乘积的比值关系．
（2）利用推导出的水的质量与比热容的乘积和金属球的质量与比热容的乘积的比值关系，结合第二次热传递求出乙容器中水的温度．
（2）利用推导出的水的质量与比热容的乘积和金属球的质量与比热容的乘积的比值关系，结合第二次热传递求出乙容器中水的温度．
解答：解：
①当将金属球放入甲容器中时，金属球放出的热量与水吸收的热量相等，即：Q金=Q水．
设金属球的质量为m金、比热容为c金、水的质量为m水、水的比热容为c水
则：Q金=m金×c金（65℃-45℃），Q水=m水×c水（45℃-25℃）
因为：Q金=Q水
所以：m金×c金（65℃-45℃）=m水×c水（45℃-25℃）
化简得：
=
；
②当将金属球放入乙容器中时，乙容器中的水放出的热量与金属球吸收的热量相等，即：Q水=Q金．
由于甲乙容器中的水的质量相等，又是同一个金属球，所以仍设金属球的质量为m金、比热容为c金、水的质量为m水、水的比热容为c水，此时两者共同的温度为t℃
则：Q水=m水×c水（75℃-t℃），Q金=m金×c金（t℃-45℃）
因为：Q水=Q金
即：m水×c水（75℃-t℃）=m金×c金（t℃-45℃），
∴75℃-t℃=t℃-45℃
解得：t=60℃
故选B．
①当将金属球放入甲容器中时，金属球放出的热量与水吸收的热量相等，即：Q金=Q水．
设金属球的质量为m金、比热容为c金、水的质量为m水、水的比热容为c水
则：Q金=m金×c金（65℃-45℃），Q水=m水×c水（45℃-25℃）
因为：Q金=Q水
所以：m金×c金（65℃-45℃）=m水×c水（45℃-25℃）
化简得：
| c水m水 |
| c金m金 |
| 1 |
| 1 |
②当将金属球放入乙容器中时，乙容器中的水放出的热量与金属球吸收的热量相等，即：Q水=Q金．
由于甲乙容器中的水的质量相等，又是同一个金属球，所以仍设金属球的质量为m金、比热容为c金、水的质量为m水、水的比热容为c水，此时两者共同的温度为t℃
则：Q水=m水×c水（75℃-t℃），Q金=m金×c金（t℃-45℃）
因为：Q水=Q金
即：m水×c水（75℃-t℃）=m金×c金（t℃-45℃），
∴75℃-t℃=t℃-45℃
解得：t=60℃
故选B．
点评：（1）在此题中，通过前后两次是同一个球分别放入盛有质量相等的水的甲乙两个容器中，可以得到很多不变的量．即在第一次热传递中的物理量，在第二次热传递中照样可以使用．这是解决此题的关键．
（2）在此题中，不能求出这种金属球的质量和比热容，利用整体代换的思想是解决此题的突破口．
（2）在此题中，不能求出这种金属球的质量和比热容，利用整体代换的思想是解决此题的突破口．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
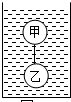（2011?平谷区二模）底面积为50cm2的容器中装有一定量的水，用轻质细绳相连的体积相同的甲、乙两球悬浮在水中，如图所示；将细绳剪断后，甲球漂浮且有
（2013?沈阳二模）水平桌面上的甲、乙两个薄壁轻质圆柱形容器，装有质量相同的水，如图所示．水对甲、乙两容器底的压力和压强的大小关系分别是：F甲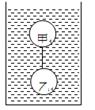
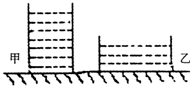水平桌面上的甲、乙两个薄壁轻质圆柱形容器，装有质量相同的水，如图所示．水对甲、乙两容器底的压力和压强的大小关系分别是：F甲________F乙；p甲________p乙；若将两个完全相同的木球分别投入甲、乙两个容器中静止后（水未溢出），水对容器底部增大的压强△p甲________△p乙． （都选填“＞”、“＜”或“=”）