Question

如图所示，三个实心匀质小球（球的体积公式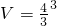）静止在液体中，甲球有一半体积在液面之上．小球的半径之比为r_甲：r_乙：r_丙=3：2：1，甲与丙的密度之比为ρ_甲：ρ_丙=1：3，则

1. A.
   三球的密度之比为：ρ_甲：ρ_乙：ρ_丙=1：2：3
2. B.
   三球所受浮力之比为：F_甲：F_乙：F_丙=27：8：2
3. C.
   三球所受重力之比为：G_甲：G_乙：G_丙=27：16：3
4. D.
   若让乙球和丙球也漂浮并都有一半体积在液面上，应该将它们挖成空心的．则这时乙球和丙球的空心体积之比为6：1

Answer 1

ACD
分析：①利用体积公式计算出体积比，然后利用密度公式计算出甲乙丙的质量比即三球所受重力比；
②甲利用漂浮的条件计算出与丙的关系，乙利用悬浮的条件计算出与丙的关系，然后计算出甲乙的空心体积比．
解答：（1）甲球漂浮，V_甲排==×π×（r_甲）³=×π×（3r_丙）³=18πr_丙³；
乙球悬浮，V_乙排=π（r_乙）³=π（2r_丙）³=πr_丙³；
丙球沉入水底，V_丙排=πr_丙³；
由F_浮=ρgV_排可知，三球所受浮力之比为：F_甲：F_乙：F_丙=27：16：2，B错误；
（2）因甲球漂和乙球悬浮，由物体的浮沉条件可知，浮力和重力相等，即F_浮=G_物，
由F_浮=ρ_液gV_排，G_物=ρ_物V_物g可知：
ρ_甲：ρ_乙=1：2；
又因ρ_甲：ρ_丙=1：3
所以ρ_甲：ρ_乙：ρ_丙=1：2：3，A正确；
（3）由G=mg=ρ_物gV，可知：
G_甲：G_乙：G_丙=ρ_甲V_甲：ρ_乙V：ρ_丙V_丙=ρ_甲×36πr_丙³：ρ_乙×πr_丙³：ρ_丙×πr_丙³=27：16：3，C正确；
（4）从题意可知，甲的密度为液体的；乙的密度等于液体密度，丙的密度为液体密度的倍；
要浮在液面一半，就是要把密度降低到液体密度的．
若让乙球和丙球也漂浮并都有一半体积在液面以上，则乙要挖掉体积的一半，而丙要挖掉，就和甲的密度一样了．
而：乙的半径是丙的2倍，体积与半径的关系是立方关系，则：
乙要挖掉的体积=V_乙×=8×V_丙×=4×V_丙
丙要挖掉的体积=V_丙×，
V_乙：V_丙=4：=6：1，故D选项正确；
故选ACD．
点评：本题涉及知识点多，易出错；涉及浮力知识，要灵活利用密度公式，重力公式，漂浮、悬浮的条件等公式计算．