题目内容
 把一根均匀电阻丝弯折成一个闭合的等边三角形abc,如图所示,图中d点为底边ab的中心.如果cd两点间的电阻为9欧姆,则( )
把一根均匀电阻丝弯折成一个闭合的等边三角形abc,如图所示,图中d点为底边ab的中心.如果cd两点间的电阻为9欧姆,则( )分析:△abc为等边三角形,设一个边的电阻为R,c、d两端的电阻为dac和dbc并联,据此可求一个边的电阻;
ac两点的电阻是ac和abc并联,根据并联电阻的特点求解;
ad两点的电阻是ad和acbd并联,根据并联电阻的特点求解.
ac两点的电阻是ac和abc并联,根据并联电阻的特点求解;
ad两点的电阻是ad和acbd并联,根据并联电阻的特点求解.
解答:解:(1)设一个边的电阻为R,
则Rdac=Rdbc=
R,
c、d两点间的电阻为Rdac和Rdbc并联,
Rcd=
×Rdac=
×
R=9Ω,
∴R=12Ω;
ac两点间的电阻是Rac和Rabc并联,如图,
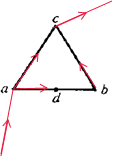
Rac=R=12Ω,Rabc=2R=24Ω,
R并=
=
=8Ω;故选项A、B错误;
(2)ad两点间的电阻是Rad和Racbd并联,
Rad=
R=
×12Ω=6Ω,Racbd=2R+
R=
R=
×12Ω=30Ω,
R并′=
=
=5Ω.故选项C正确,D错误.
故选C.
则Rdac=Rdbc=
| 3 |
| 2 |
c、d两点间的电阻为Rdac和Rdbc并联,
Rcd=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴R=12Ω;
ac两点间的电阻是Rac和Rabc并联,如图,

Rac=R=12Ω,Rabc=2R=24Ω,
R并=
| Rac×Rabc |
| Rac+Rabc |
| 12Ω×24Ω |
| 12Ω+24Ω |
(2)ad两点间的电阻是Rad和Racbd并联,
Rad=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
R并′=
| Rad×Rabcd |
| Rad+Rabdc |
| 6Ω×30Ω |
| 6Ω+30Ω |
故选C.
点评:本题考查了电阻并联的计算,能从图看出两点间的电阻为两端导线并联是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
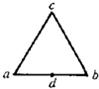 把一根均匀电阻丝弯折成一个闭合的等边三角形abc,如图所示,图中d点为底边ab的中心.如果cd两点间的电阻为9欧姆,则( )
把一根均匀电阻丝弯折成一个闭合的等边三角形abc,如图所示,图中d点为底边ab的中心.如果cd两点间的电阻为9欧姆,则( ) 把一根均匀电阻丝弯折成一个闭合的等边三角形abc,如图所示,图中d点为底边ab的中心.如果cd两点间的电阻为9欧姆,则( )
把一根均匀电阻丝弯折成一个闭合的等边三角形abc,如图所示,图中d点为底边ab的中心.如果cd两点间的电阻为9欧姆,则( )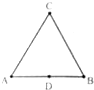 把一根均匀电阻丝弯折成一个封闭的等边三角形ABC,如图所示.图中D为AB边的中点.如果A、C之间的电阻大小为8欧,则B、D之间的电阻大小为( )
把一根均匀电阻丝弯折成一个封闭的等边三角形ABC,如图所示.图中D为AB边的中点.如果A、C之间的电阻大小为8欧,则B、D之间的电阻大小为( )