题目内容
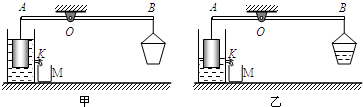
（2013?通州区模拟）杠杆AB可绕O点在竖直平面内自由转动，A端通过细绳悬挂一圆柱形金属块，B端通过细绳悬挂一质量为1kg的小桶．当金属块刚刚浸没在圆柱形容器内的水中时，杠杆在水平位置平衡，如图甲所示．打开圆柱形容器侧壁的阀门K，放出适量水到烧杯M中，然后关闭阀门，把放出的水全部倒入小桶中，杠杆在水平位置又重新平衡，如图乙所示．已知圆柱形金属块的底面积为60cm2、高为5cm，圆柱形容器的底面积为100cm2，g取10N/kg．不计杠杆及细绳质量，则金属块的密度为
6×103
6×103
kg/m3．分析：对圆柱金属体受力分析可知，受竖直向上的拉力和浮力、竖直向下的重力，根据力的平衡求出绳子的拉力，利用力的相互作用可知，此时的拉力即为绳子对A点的力；
根据阿基米德原理和杠杆的平衡条件得出放水前后的等式，解等式即可求出金属块的质量，根据密度公式求出金属块的密度．
根据阿基米德原理和杠杆的平衡条件得出放水前后的等式，解等式即可求出金属块的质量，根据密度公式求出金属块的密度．
解答：解：根据杠杆的平衡条件和阿基米德原理可得：
由图甲可得：（m金g-ρ水gS金H）L1=m桶gL2-------①
设水面下降的高度h，则
此时金属块排开水的体积V排=S金（H-h）---------②
排出水的体积V水=（S容器-S金）h-------------③
由图乙可得：（m金g-ρ水gV排）L1=（m桶g+ρ水V水g）L2------④
由②③代入④可得：
[m金g-ρ水gS金（H-h）]L1=[m桶g+ρ水（S容器-S金）hg]L2------⑤
由①和⑤相比可得：
m金=
+ρ水gS金H=
+1.0×103kg/m3×10N/kg×60×10-4m2×5×10-2m=1.8kg，
金属的体积V金=S金H=60cm2×5cm=3×10-4m3，
金属的密度：ρ金=
=
=6×103kg/m3．
故答案为：6×103．
由图甲可得：（m金g-ρ水gS金H）L1=m桶gL2-------①
设水面下降的高度h，则
此时金属块排开水的体积V排=S金（H-h）---------②
排出水的体积V水=（S容器-S金）h-------------③
由图乙可得：（m金g-ρ水gV排）L1=（m桶g+ρ水V水g）L2------④
由②③代入④可得：
[m金g-ρ水gS金（H-h）]L1=[m桶g+ρ水（S容器-S金）hg]L2------⑤
由①和⑤相比可得：
m金=
| m金S金 |
| S容-S金 |
| 1kg×60×10-4m2 |
| (100-60)×10-4m2 |
金属的体积V金=S金H=60cm2×5cm=3×10-4m3，
金属的密度：ρ金=
| m金 |
| V金 |
| 1.8kg |
| 3×10-4m3 |
故答案为：6×103．
点评：本题考查了学生对重力公式、阿基米德原理、压强公式、杠杆的平衡条件的掌握和运用，得出放出水的体积和此时排水的体积是突破口，利用好杠杆平衡条件是本题的关键．
练习册系列答案
相关题目
（2013?通州区一模）如图所示的电路中，电源两端电压不变，灯的电阻不变．当开关S1闭合，S2断开，滑动变阻器的滑片P移到B端时，R1的电功率为P1，电流表示数为I1；当开关S1断开，S2 闭合时，R1 的电功率为 P′1，电流表示数为I2，此时灯L正常发光；当开关S1、S2 都断开，滑动变阻器的滑片P在C点时，变阻器接入电路的电阻为RC，RC 的电功率为PC，电压表V1的示数为U1，电压表V2的示数为U2，已知U1：U2=3：2，
（2013?通州区一模）小华想利用电流表和阻值已知的电阻R0测量电阻Rx的电阻值．他选择了满足实验要求的电源、电流表，并连接了部分实验电路，如图所示．
（2013?通州区一模）小航在实验室测量盐水密度．小航先将适量盐水倒入烧杯，用天平测量烧杯和盐水的总质量，天平平衡时的情景如图甲所示，则烧杯和盐水的总质量为