题目内容
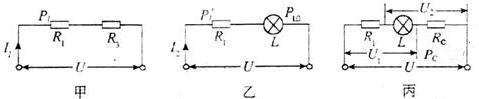
 (2013?通州区一模)如图所示的电路中,电源两端电压不变,灯的电阻不变.当开关S1闭合,S2断开,滑动变阻器的滑片P移到B端时,R1的电功率为P1,电流表示数为I1;当开关S1断开,S2 闭合时,R1 的电功率为 P′1,电流表示数为I2,此时灯L正常发光;当开关S1、S2 都断开,滑动变阻器的滑片P在C点时,变阻器接入电路的电阻为RC,RC 的电功率为PC,电压表V1的示数为U1,电压表V2的示数为U2,已知U1:U2=3:2,
(2013?通州区一模)如图所示的电路中,电源两端电压不变,灯的电阻不变.当开关S1闭合,S2断开,滑动变阻器的滑片P移到B端时,R1的电功率为P1,电流表示数为I1;当开关S1断开,S2 闭合时,R1 的电功率为 P′1,电流表示数为I2,此时灯L正常发光;当开关S1、S2 都断开,滑动变阻器的滑片P在C点时,变阻器接入电路的电阻为RC,RC 的电功率为PC,电压表V1的示数为U1,电压表V2的示数为U2,已知U1:U2=3:2,I1:I2=3:5,灯的额定功率为8W.电路通过断开、闭合开关以及移动滑动变阻器的滑片P,形成的不同电路所消耗的最大电功率与最小电功率之比为3:1.求:
(1)P1与P′1的比值
(2)电阻R1与滑动变阻器最大阻值之比
(3)滑动变阻器的电功率PC.
分析:(1)当S1闭合、S2断开,滑片P在B端时,R3连入电路中的阻值最大,L被短路,R1和R3组成串联电路;当S1断开、S2闭合时,灯正常发光,R3被短路,R1和L组成串联电路,而两次R1的阻值保持不变,可利用电流I1与I2的比值和P=I2R求出P1与P′1的比值.
(2)当S1和S2都断开,滑片P在B端时,R1、R2、L组成串联电路,总电阻最大,总功率Pmin,当S1和S2都闭合时,电路中只有R1,总电阻最小,总功率Pmax.电源的电压不变,可利用公式
=
求电阻R1与滑动变阻器最大阻值之比.
(3)先求出RC、RL之间的关系,当S1断开、S2闭合时,灯正常发光,R3被短路,R1和L组成串联电路,根据P=I2R求出此时的总功率,再根据电源的电压不变求出当S1、S2都断开,滑片P在C时电路的总功率,利用此时电路中电阻之间的关系求出滑动变阻器的电功率.
(2)当S1和S2都断开,滑片P在B端时,R1、R2、L组成串联电路,总电阻最大,总功率Pmin,当S1和S2都闭合时,电路中只有R1,总电阻最小,总功率Pmax.电源的电压不变,可利用公式
| Pmax |
| Pmin |
| Rmax |
| Rmin |
(3)先求出RC、RL之间的关系,当S1断开、S2闭合时,灯正常发光,R3被短路,R1和L组成串联电路,根据P=I2R求出此时的总功率,再根据电源的电压不变求出当S1、S2都断开,滑片P在C时电路的总功率,利用此时电路中电阻之间的关系求出滑动变阻器的电功率.
解答:解:当S1闭合、S2断开,滑片P在B端时,电路如图甲所示;当S1断开、S2闭合时,灯正常发光,电路如图乙所示;
当S1、S2都断开,滑片P在C时,电路如图丙所示.
(1)∵
=
,
∴
=
=(
)2=
;
(2)当S1和S2都断开,滑片P在B端时,电路如图(A),总电阻最大,总功率Pmin;
当S1和S2都闭合时,电路如图(B),总电阻最小,总功率Pmax.

∵电源的电压不变,
∴
=
=
=
,
∴2R1=RL+R3----------------①
由甲、乙可知,电源的电压不变时,则有:
=
=
,
∴2R1=3R3-5RL------------②
由①②两式可得:3RL=R3,R1=2RL,
∴
=
.
(3)由图丙可知:
=
=
,
∴2R1=RL+3RC--------------③
将R1=2RL代入③式得:RC=RL,
由乙图可知,此时电路的总功率为P乙=
PL=3PL=3×8W=24W,
因电源的电压不变由乙丙两图可得:
=
=
,
所以丙图的总功率为:P丙=
P乙=18W,
所以PC=
P丙=
P丙=4.5W
答:(1)P1与P′1的比值为9:25;
(2)电阻R1与滑动变阻器最大阻值之比为2:3;
(3)滑动变阻器的电功率PC的功率为4.5W.
当S1、S2都断开,滑片P在C时,电路如图丙所示.

(1)∵
| I1 |
| I2 |
| 3 |
| 5 |
∴
| P1 |
| P1′ |
| ||
|
| I1 |
| I2 |
| 9 |
| 25 |
(2)当S1和S2都断开,滑片P在B端时,电路如图(A),总电阻最大,总功率Pmin;
当S1和S2都闭合时,电路如图(B),总电阻最小,总功率Pmax.

∵电源的电压不变,
∴
| Pmax |
| Pmin |
| Rmax |
| Rmin |
| R1+RL+R3 |
| R1 |
| 3 |
| 1 |
∴2R1=RL+R3----------------①
由甲、乙可知,电源的电压不变时,则有:
| I1 |
| I2 |
| R1+RL |
| R1+R3 |
| 3 |
| 5 |
∴2R1=3R3-5RL------------②
由①②两式可得:3RL=R3,R1=2RL,
∴
| R1 |
| R3 |
| 2 |
| 3 |
(3)由图丙可知:
| U1 |
| U2 |
| R1+RL |
| RL+RC |
| 3 |
| 2 |
∴2R1=RL+3RC--------------③
将R1=2RL代入③式得:RC=RL,
由乙图可知,此时电路的总功率为P乙=
| R1+RL |
| RL |
因电源的电压不变由乙丙两图可得:
| P丙 |
| P乙 |
| R1+RL |
| R1+RL+RC |
| 3 |
| 4 |
所以丙图的总功率为:P丙=
| 3 |
| 4 |
所以PC=
| RC |
| R1+RL+RC |
| 1 |
| 4 |
答:(1)P1与P′1的比值为9:25;
(2)电阻R1与滑动变阻器最大阻值之比为2:3;
(3)滑动变阻器的电功率PC的功率为4.5W.
点评:本题考查了学生对串、并联电路的辨别和串联电路的特点以及欧姆定律的应用.本题难点是很多同学无法将三种状态下的电流关系及电压关系联系在一起,故无法找到突破口.解答此类问题时,可将每一种情况中的已知量和未知量都找出来,仔细分析找出各情况中的关联,即可列出等式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (2013?通州区一模)实验桌上现有如下器材:符合要求的电源,电阻箱(电路图符号
(2013?通州区一模)实验桌上现有如下器材:符合要求的电源,电阻箱(电路图符号 )1个,已调零的电流表1块,刻度尺1把,粗细均匀、横截面积为1mm2的合金丝1盘,开关2个,带有金属夹的导线若干.请使用现有的实验器材,设计实验证明:导体电阻的大小与导体长度成正比.(在电路图中合金丝用电阻的符号表示)
)1个,已调零的电流表1块,刻度尺1把,粗细均匀、横截面积为1mm2的合金丝1盘,开关2个,带有金属夹的导线若干.请使用现有的实验器材,设计实验证明:导体电阻的大小与导体长度成正比.(在电路图中合金丝用电阻的符号表示) (2013?通州区一模)如图是某种健身器材局部结构示意图,物体A恰好被竖直滑道夹紧.在滑轮组绳子的自由端施加竖直向下的拉力F1,物体A恰能沿竖直滑道向下做匀速直线运动;在滑轮组绳子的自由端施加竖直向下的拉力F2,物体A恰能以速度v1竖直向上做匀速直线运动,此时滑轮组的机械效率为η1;在物体A下加挂一个物体B(B不与滑道相接触),在滑轮组绳子的自由端施加竖直向下的力F3,则物体A和B恰能以速度v2竖直向上做匀速直线运动,此时滑轮组的机械效率为η2.已知物体A所受重力GA=355N,F1:F2=40:41,η1:η2=81:82,当F2做82J的功时,物体A升高了0.2m.若物体A沿滑道运动过程中所受摩擦力大小始终不变,且不计绳重及滑轮轴的摩擦.求:
(2013?通州区一模)如图是某种健身器材局部结构示意图,物体A恰好被竖直滑道夹紧.在滑轮组绳子的自由端施加竖直向下的拉力F1,物体A恰能沿竖直滑道向下做匀速直线运动;在滑轮组绳子的自由端施加竖直向下的拉力F2,物体A恰能以速度v1竖直向上做匀速直线运动,此时滑轮组的机械效率为η1;在物体A下加挂一个物体B(B不与滑道相接触),在滑轮组绳子的自由端施加竖直向下的力F3,则物体A和B恰能以速度v2竖直向上做匀速直线运动,此时滑轮组的机械效率为η2.已知物体A所受重力GA=355N,F1:F2=40:41,η1:η2=81:82,当F2做82J的功时,物体A升高了0.2m.若物体A沿滑道运动过程中所受摩擦力大小始终不变,且不计绳重及滑轮轴的摩擦.求: