题目内容
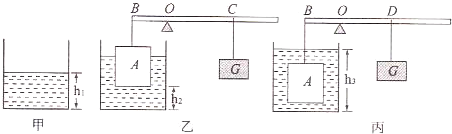
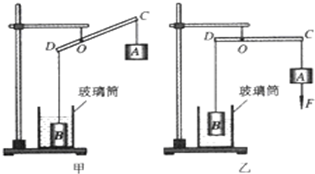
如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体B浸没在水中,杠杆CD可绕支点O在竖直平面内转动,CO=2DO;物体A是质量为100g的配重物.在物体A上再加一个0.6N的向下拉力F,杠杆会转动到在水平位置平衡,如图乙所示,此时物体B有
的体积露出水面,筒中水的深度比图甲中水的深度下降了0.4cm.(取10N/kg,杠杆、悬挂物体的细绳的质量均忽略计)
求:(1)物体B的体积;
(2)乙图中物体B所受的浮力大小;
(3)乙图中物体B底部所受水的压强大小;
(4)物体B的密度.
| 2 | 5 |

求:(1)物体B的体积;
(2)乙图中物体B所受的浮力大小;
(3)乙图中物体B底部所受水的压强大小;
(4)物体B的密度.
分析:由玻璃筒内液面高度的变化可求出排开水的体积及物体的体积,进而可求出物体所受浮力,由杠杆在水平位置平衡可得物体的重力,由物体质量和体积可求得密度.
解答:已知:筒的底面积为S筒=50cm2=50×10-4m2,圆柱形物体B的底面积为SB=10cm2=10×10-4m2,CO=2DO;物体A是质量为mA=100g=0.1kg,向下拉力F=0.6N,V排=
V,△h=0.4cm=0.4×10-2m,g=10N/kg
求:(1)物体B的体积VB=?;(2)物体B所受的浮力大小F浮=?;(3)物体B底部所受水的压强大小p=?;(4)物体B的密度ρB=?
解:(1)由题意知:物体
的体积露出水面时,水面下降的体积为V1=S筒×△h=50×10-4m2×0.4×10-2m=2×10-5m3,
即物体的
体积为2×10-5m3,则物体的体积为:VB=
=5×10-5m3=50cm3;
(2)平衡时物体所受浮力为:F浮=ρg
V=1.0×103kg/m3×10N/Kg×
×5×10-5m3=0.3N;
(3)由浮力的形成知:F向上=F浮=pSB,
则p=
=
=
=300Pa;
(4)由杠杆平衡条件得:
(GB-F浮)×DO=(GA+F)×CO,
(GB-0.3N)=(mAg+0.6N)×2
GB=(0.1kg×10N/kg+0.6N)×2+0.3N=3.5N,
∵G=mg
∴B物体的质量mB=
=
=0.35kg=350g,
物体B的密度ρB=
=
=7g/cm3=7×103kg/m3.
答:(1)物体B的体积为5×10-5m3;
(2)物体B所受的浮力大小为0.3N;
(3)物体B底部所受水的压强大小为300Pa;
(4)物体B的密度为7×103kg/m3.
| 3 |
| 5 |
求:(1)物体B的体积VB=?;(2)物体B所受的浮力大小F浮=?;(3)物体B底部所受水的压强大小p=?;(4)物体B的密度ρB=?
解:(1)由题意知:物体
| 2 |
| 5 |
即物体的
| 2 |
| 5 |
| 2×10-5m3 | ||
|
(2)平衡时物体所受浮力为:F浮=ρg
| 3 |
| 5 |
| 3 |
| 5 |
(3)由浮力的形成知:F向上=F浮=pSB,
则p=
| F向上 |
| SB |
| F浮 |
| SB |
| 0.3N |
| 10×10-4m2 |
(4)由杠杆平衡条件得:
(GB-F浮)×DO=(GA+F)×CO,
(GB-0.3N)=(mAg+0.6N)×2
GB=(0.1kg×10N/kg+0.6N)×2+0.3N=3.5N,
∵G=mg
∴B物体的质量mB=
| GB |
| g |
| 3.5N |
| 10N/kg |
物体B的密度ρB=
| mB |
| VB |
| 350g |
| 50cm3 |
答:(1)物体B的体积为5×10-5m3;
(2)物体B所受的浮力大小为0.3N;
(3)物体B底部所受水的压强大小为300Pa;
(4)物体B的密度为7×103kg/m3.
点评:本题考查内容较多,计算量较大,在做题时力争能先进行细化逐个突破.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
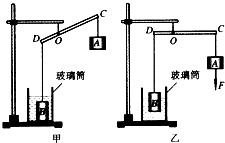 如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体B浸没在水中,杠杆CD可绕支点O在竖直平面内转动,CO=2DO;物体A是质量100g的配重.如图乙所示,杠杆在水平位置平衡,作用在物体A上的方向向下的拉力F为0.6N,物体B有
如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体B浸没在水中,杠杆CD可绕支点O在竖直平面内转动,CO=2DO;物体A是质量100g的配重.如图乙所示,杠杆在水平位置平衡,作用在物体A上的方向向下的拉力F为0.6N,物体B有| 2 |
| 5 |
| A、P的大小为500Pa |
| B、F浮的大小为0.2N |
| C、物体B的密度为7g/cm3 |
| D、物体B的体积为100cm3 |
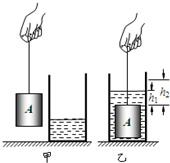 如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是
如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是