题目内容
2012年10月15日,奥地利著名极限运动员鲍姆加特纳乘坐热气球从距地面高度约39km的高空跳下,并成功着陆.如图所示.该热气球由太空舱,绳索和气囊三部分组成.气囊与太空舱之间利用绳索连接.在加热过程中气囊中气体受热膨胀.密度变小,一部分气体逸出,当热气球总重力小于浮力时便开始上升.
假定鲍姆加特纳是在竖直方向上运动的,并经历了以下几个运动阶段:他首先乘坐热气球从地面开始加速上升到离地高h1=1km处,此阶段绳索对太空舱向上的总拉力恒为F1=3002.5N;接着再匀速上升到离地面高h2=38km处,此阶段绳索对太空舱向上的总拉力恒为F2=3000N;然后再减速上升到离地高h3=39km处,此阶段绳索对太空舱向上的总拉力恒为F3=2997.5N;他在上升过程中共用时t1=1×104s,在离地高39km处立即跳下.自由下落t2=4min后速度已超过音速,最后打开降落伞,又用时t3=16min又安全到达地面.忽略髙度对g的影响,取g=10N/kg.求:
①从离开地面到安全返回地面的整个过程中,运动员的平均速度是多少?(结果取整数)
②在热气球上升过程中.绳索对太空舱向上的总拉力做功的平均功率是多少?
③当热气球上升到离地高20km处.若热气球总质量(含气囊里面气体)m=7.18×104kg,整个热气球的体积V=8×105m3,整个热气球受到的空气阻力f=2×103N,不考虑气流(或风) 对热气球的影响.则此高度处的空气密度是多少?
①7m/s;②1.17×104W;③0.09kg/m3.
解析试题分析:①从离开地面到安全返回地面的过程中,运动员的总路程为s=2h3=2×39km=78km=7.8×104m;
从离开地面到安全返回地面的过程中,运动员的总时间t=t1+t2+t3=1×104s+4×60s+16×60s=1.12×104s;
从离开地面到安全返回地面的过程中,运动员的平均速度为v= =7m/s.
=7m/s.
②在热气球上升阶段,绳索对太空舱向上的总拉力做功有三个阶段:
第一阶段:W1=F1h1=3002.5N×1000m=3.0025×106J,
第二阶段:W2=F2(h2﹣h1)=3000N×(38000m﹣1000m)=1.11×108J,
第三阶段:W3=F3(h3﹣h2)=2997.5N×(39000m﹣38000m)=2.9975×106J;
上升过程中拉力共做功W=W1+W2+W3=3.0025×106J+1.11×108J+2.9975×106J=1.17×108J,
在整个上升过程中总拉力的平均功率为P=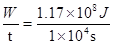 =1.17×104W;
=1.17×104W;
③当热气球上升到离地高20km处.热气球的总重力为G=mg=7.18×104kg×10N/kg=7.18×105N,
此时热球匀速上升,受平衡力作用,热气球受到的空气浮力为F浮=G+f=7.18×105N+2×103N=7.2×105N,
而F浮=ρ空气gV排,得空气的密度为ρ空气=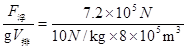 =0.09kg/m3.
=0.09kg/m3.
考点:变速运动的平均速度;二力平衡条件的应用;功率的计算;阿基米德原理;

如图,工人要将一块重900N的建材运到10m高处,装置中每个滑轮重100N,建材上升的速度是0.8m/s.在施工过程中,下列说法正确的是: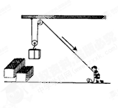
| A.工人的拉力为500N | B.工人拉绳的速度为2.4m/s |
| C.工人做功的功率为400W | D.工人做功的机械效率小于90% |
我国第一艘航空母舰“辽宁号”已投入使用,飞机可以在舰上起降,下面说法中不正确的是( )
| A.飞机是用密度较小的新材料制造的 |
| B.飞机的机翼是根据伯努利原理设计的 |
| C.飞机在航母上起飞时,航母相对于飞机是静止的 |
| D.航空母舰上安装的雷达是利用电磁波来发现军事目标的 |
小青是一名九年级同学,他对自身相关的物理量估测中明显不合理的是 ( )
| A.跳高的成绩约为1.2m |
| B.百米赛跑的成绩约为14s |
| C.自身的质量大小约为45kg |
| D.自身的平均密度约为0.7×103 kg/ m3 |
学校举行初三年级排球比赛,激发了同学们对排球有关问题的讨论.下列说法中错误的是( )
| A.排球从空中下落,速度逐渐加快,其重力势能转化为动能 |
| B.静止在水平地面上的排球,它所受的重力与排球对地面的压力是一对平衡力 |
| C.扣球时,手感觉有点痛,说明力的作用是相互的 |
| D.排球被网弹回,是力改变了排球的运动状态 |




