题目内容
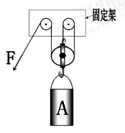
(共5分)如下图甲所示,小明在探究“杠杆的平衡条件”实验中所用的实验器材有:杠杆、支架、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。

(1)实验前,将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉.此时,应把杠杆左端的平衡螺母向 (填“左”或“右”)调节,使杠杆在不挂钩码时,达到水平平衡状态。
(2)杠杆调节平衡后,小明在杠杆上A点处挂4个钩码,在B点处挂6个钩码杠杆恰
好在原位置平衡。于是小明便根据这次实验得出了杠杆的平衡条件为F1l1= F2l2。他这样
得出的结论是否合理? ;理由是: 。
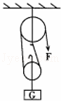
(3)实验结束后,小明提出了新的探究问题:“若支点不在杠杆的中点时,杠杆的平衡条件是否仍然成立?”于是小组同学利用如图乙所示装置进行探究,发现在杠杆左端的不同位置,用弹簧测力计竖直向上拉使杠杆处于水平平衡时,测出的拉力大小都与杠杆平衡条件不相符.其原因可能是:
。
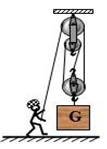
(4)如图丙所示,长1.6m、粗细均匀的金属杆可以绕O点在竖直平面内自由转动,一个“拉力──距离传感器”竖直作用在杆上,并能使杆始终保持水平平衡。该传感器显示其拉力F与作用点到O点距离x的变化关系如图丙中图像所示。可知该金属杆重 N。
(1)左.
(2)不合理,只通过一次测量,数据具有偶然性,不具备普遍性.
(3)杠杆的重心不在支点上,杠杆的重力对杠杆转动产生了影响,导致拉力F的大小比由杠杆平衡条件计算出来的数值偏大.
(4)10.
解析试题分析:(1)杠杆重心左移,应将平衡螺母(左端和右端的均可)向左调节,直至重心移到支点处,使杠杆重力的力臂为零,这样就减小了杠杆的自重对实验的影响;力臂等于支点到力的作用线的距离,当杠杆在水平位置平衡时,力的方向与杠杆垂直,力臂可以从杠杆标尺刻度上直接读出来.
(2)杠杆的平衡条件是:动力×动力臂=阻力×阻力臂(或F1L1=F2L2),只通过一次测量,数据具有偶然性,不具备普遍性.
(3)图2中,杠杆的重心不在支点上,杠杆的重力对杠杆转动产生了影响,导致拉力F的大小比由杠杆平衡条件计算出来的数值偏大.
故答案为:(1)左、水平、力臂;
(2)动力×动力臂=阻力×阻力臂(或F1L1=F2L2)、不合理、结论具有偶然性(结论没有普遍性);
(3)杠杆自重的影响.
(4)杠杆平衡条件的计算公式是:F1L1=F2L2;
金属杆重心在中心上,阻力臂为L2=0.8m,取图象上的一点F=20N,L1=0.4m,
根据杠杆的平衡条件:动力×动力臂=阻力×阻力臂
FL1=GL2
∴20N×0.4m=G×0.8m
解得:G=10N
考点:杠杠及其应用

 阅读快车系列答案
阅读快车系列答案小华在探究影响浮力大小因素的实验中,先在空气中测出圆柱体的重力大小是1.0N,然后将圆柱体逐渐浸入水中,如图甲所示,她测得圆柱体受到的浮力F和其底面进入水中的深度h的对应数据如下表:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| h/cm | 2 | 4 | 6 | 8 | 10 | 12 |
| F/N | 0.2 | 0.4 | 0.6 | 0.6 | 0.6 | 0.6 |
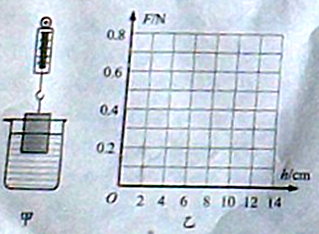
(1)第1次实验时弹簧测力计的示数为 N;
(2)利用表中数据,在图乙中画出F-h图线;
(3)当h= cm时,圆柱体刚好全部浸没水中;
(4)如改用浓盐水做实验,在图乙中再画出F-h图线。图线上h=6cm点的位置变 (高/低),这样的比较是为了探究 对浮力大小的影响。
基本实验回顾.
⑴ 在装着红棕色二氧化氮气体的瓶子上面(二氧化氮的密度大于空气密度),倒扣一个空瓶子,使两个瓶口相对,两瓶口之间用一块玻璃板隔开(图甲).抽掉玻璃板后,最终发现两瓶内气体颜色基本相同(图乙).这是一种 现象,它说明了 .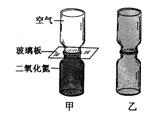
⑵在探究“导体的电阻大小与横截面积有什么关系”的实验中,请你根据下表所提供的信息,选出合适的金属丝.答: 和 .(填编号)
| 编号 | 材料 | 长度/m | 横截面积/mm2 |
| A | 镍铬合金 | 0.5 | 0.5 |
| B | 镍铬合金 | 1.0 | 0.5 |
| C | 镍铬合金 | 0.5 | 1.0 |
| D | 锰铜合金 | 0.5 | 0.5 |

⑷如图所示,用滑轮组将物块从位置A匀速拉到位置B,请在图中画出最省力的绕线方法.