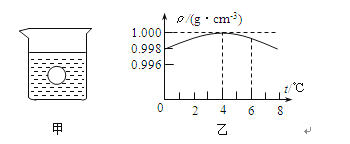题目内容
【题目】底面积为S0的圆柱形薄壁容器内装有密度为ρ0的液体,横截面积为S1的圆柱形木块由一段非弹性细线与容器底部相连,且部分浸入液中,此时细线刚好伸直,如图所示.已知细线所能承受的最大拉力为T,现往容器中再缓慢注入密度为ρ0的液体,直到细线刚好被拉断为止.请解答下列问题;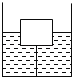
(1)画出细线刚好伸直时,木块在竖直方向上的受力示意图;
(2)导出细线未拉断前,细线对木块拉力F与注入的液体质量m之间的关系式;
(3)求出细线刚好被拉断时与细线断后容器中液面恢复稳定时,容器底部所受液体压强的变化量.
【答案】
(1)
解:细线刚好伸直时,木块受到重力和浮力作用,二力平衡,大小相等,力的作用点画在重心上,如图所示:
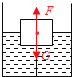
(2)
解:注入液体的质量为m时,细线对木块的拉力为F,液面上升的高度为△h,
细线对木块的拉力F等于木块增大的浮力,则有:
F=△F浮=ρ0gV排=ρ0gS1△h,①
由ρ=![]() 得,容器内注入的液体质量:
得,容器内注入的液体质量:
m=ρ0V液=ρ0(S0﹣S1)△h,②
将①式和②式联立,解得:
F=![]() m;
m;
答:导出细线未拉断前,细线对木块拉力F与注入的液体质量m之间的关系式为:F=![]() m;
m;
(3)
解:
当细线刚好被拉断时,F浮=G+T,
液面恢复稳定后,F浮′=G,
即:F浮﹣F浮′=T,
ρ0g(V排﹣V排′)=T
ρ0g△h′S0=T
△p=![]() .
.
答:求出细线刚好被拉断时与细线断后容器中液面恢复稳定时,容器底部所受液体压强的变化量为△p=![]() .
.
【解析】(1)细线刚好伸直时,木块竖直方向上受到重力和浮力作用,二力平衡,大小相等,根据力的示意图画法,画出二力的示意图;
(2)随着液面的上升,浮力增大,绳子的拉力增大,细线的拉力F等于增大的浮力,即F=△F浮=ρ0gV排 , ;由密度公式ρ=![]() 的变形公式m=ρV和体积公式V=Sh表示出容器内注入的液体质量,二式联立可得到细线对木块拉力F与注入的液体质量m之间的关系式;
的变形公式m=ρV和体积公式V=Sh表示出容器内注入的液体质量,二式联立可得到细线对木块拉力F与注入的液体质量m之间的关系式;
(3)细线刚好被拉断时,木块受到重力、浮力和细线的拉力,其关系式为F浮=G+T;细线断后容器中液面恢复稳定时,木块漂浮,F![]() =G;将二式联立,根据阿基米德原理和压强计算公式,得出容器底部所受液体压强的变化量.
=G;将二式联立,根据阿基米德原理和压强计算公式,得出容器底部所受液体压强的变化量.
【考点精析】掌握力的合成与应用和阿基米德原理是解答本题的根本,需要知道如果已知几个力的大小和方向,求合力的大小和方向称为力的合成.(求合力时,一定要注意力的方向) 注意:同一直线上的两个力,方向相同时,合力必大于其中的任何一个力.方向相反的两个力,大小相等时,合力为0;大小不等时,合力一定小于较大的力,可能大于较小的力,也可能小于较小的力;阿基米德原理:浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开的液体所受的重力.这个规律叫做阿基米德原理,即 F浮= G排 =ρ液gv排.

【题目】为了测量某种食用油的密度,取适量这种食用油进行如下实验: ( 1 )将托盘天平放在水平桌面上,把游码移到标尺左端的刻度线处,发现指针静止时如图甲所示,则应将平衡螺母向(选填“左“或“右”)调节使横梁平衡.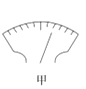
( 2 )向烧杯中倒入适量的食用油,用天平测量烧杯和食用油的总质量m1 , 天平平衡时,砝码和游码的位置如图乙所示.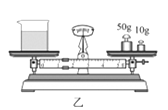
( 3 )把烧杯中的部分食用油倒入量筒中,其示数如图丙所示.![]()
( 4 )测出烧杯和剩余食用油的总质量m2为26g.
( 5 )请将数据及计算结果填在表中.
烧杯和食用油的总质量m1/g | 烧杯和剩余食 | 量筒中食用油的质量 | 量筒中食用油的体积 | 食用油的密度 |
26 |