题目内容
 在课外小组活动中,小刚将一挂在弹簧测力计下的不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示.求:
在课外小组活动中,小刚将一挂在弹簧测力计下的不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示.求:(1)石块在水中所受到的浮力.
(2)石块的密度;
(3)盐水的密度;
(4)小婷将一底面积为10cm2的实心金属圆柱体挂在弹簧测力计下,缓慢浸没到底面积为40cm2的薄壁盛水圆柱形容器中(水未溢出且物体未接触容器底部),弹簧测力计示数改变了2N,则容器底部对水平桌面的压强改变了多少?
分析:(1)在空气中称石块重,从甲图读出弹簧测力计的示数(石块重),从乙图读出石块全浸入水中弹簧测力计的示数,利用称重法可求出石块受到的浮力;
(2)利用阿基米德原理求石块的体积,最后利用密度公式即可求出石块的密度;
(3)利用称重法求出石块受到盐水的浮力,再利用阿基米德原理求盐水的密度.
(4)浸没水中后,测力计的示数改变了△F=2N,也就是说圆柱体受到的浮力为2N;根据公式F浮=ρ水gv排也就知道了排开液体的体积;从而知道了圆柱体的体积;又知道圆柱形容器的底面积,可以求出圆柱体浸没后水面上升的高度,再利用公式p=ρ水g△h求水对容器底部的压强增大值.
(2)利用阿基米德原理求石块的体积,最后利用密度公式即可求出石块的密度;
(3)利用称重法求出石块受到盐水的浮力,再利用阿基米德原理求盐水的密度.
(4)浸没水中后,测力计的示数改变了△F=2N,也就是说圆柱体受到的浮力为2N;根据公式F浮=ρ水gv排也就知道了排开液体的体积;从而知道了圆柱体的体积;又知道圆柱形容器的底面积,可以求出圆柱体浸没后水面上升的高度,再利用公式p=ρ水g△h求水对容器底部的压强增大值.
解答:解:(1)由甲图可知,石块的重力为4N;
由甲乙两图得:石块在水中所受到的浮力:
F浮=G-F示=4N-3N=1N;
石块浸没在水中所受到的浮力F浮=1N,
(2)∵F浮=ρ水V排g,
∴石块的体积:
V=V排=
=
=1×10-4m3,
则石块的密度:ρ石=
=
=
=4×103kg/m3;
(3)由甲丙两图可知,石块受到盐水的浮力:
F浮′=4N-2.9N=1.1N,
∵F浮′=ρ盐水v排g,
∴ρ盐水=
=
=1.1×103kg/m3.
(4)∵弹簧测力计示数改变了2N,
则圆柱体受到水的浮力:F浮=△F=2N,
∵圆柱体浸没于水中,根据F浮=ρ水gV排
∴圆柱体排开水的体积:
V排=
=
=2×10-4m3,
将圆柱体浸没于水中后,容器内水面上升的高度h:
△h=
=
=0.05m;
水对容器底部的压强增大值:
△p=ρ水g△h=1×103kg/m3×10N/kg×0.05m=500Pa.
答:(1)石块在水中所受到的浮力为1N.
(2)石块的密度为4×103kg/m3;
(3)盐水的密度为1.1×103kg/m3.
(4)容器底部对水平桌面的压强改变了500Pa.
由甲乙两图得:石块在水中所受到的浮力:
F浮=G-F示=4N-3N=1N;
石块浸没在水中所受到的浮力F浮=1N,
(2)∵F浮=ρ水V排g,
∴石块的体积:
V=V排=
| F浮 |
| ρ水g |
| 1N |
| 1.0×103kg/m3×10N/kg |
则石块的密度:ρ石=
| m石 |
| V |
| ||
| V |
| ||
| 1×10-4m3 |
(3)由甲丙两图可知,石块受到盐水的浮力:
F浮′=4N-2.9N=1.1N,
∵F浮′=ρ盐水v排g,
∴ρ盐水=
| F浮′ |
| V排g |
| 1.1N |
| 1×10-4m3×10N/kg |
(4)∵弹簧测力计示数改变了2N,
则圆柱体受到水的浮力:F浮=△F=2N,
∵圆柱体浸没于水中,根据F浮=ρ水gV排
∴圆柱体排开水的体积:
V排=
| F浮 |
| ρ水g |
| 2N |
| 1.0×103kg/m3×10N/kg |
将圆柱体浸没于水中后,容器内水面上升的高度h:
△h=
| V排 |
| S2 |
| 2×10-4m3 |
| 40×10-4m2 |
水对容器底部的压强增大值:
△p=ρ水g△h=1×103kg/m3×10N/kg×0.05m=500Pa.
答:(1)石块在水中所受到的浮力为1N.
(2)石块的密度为4×103kg/m3;
(3)盐水的密度为1.1×103kg/m3.
(4)容器底部对水平桌面的压强改变了500Pa.
点评:本题考查学生对阿基米德原理、称重法测浮力的掌握和运用.关键是公式及其变形的灵活运用,还要注意单位的换算.本题考查了液体压强的计算、阿基米德原理、称重法测量圆柱体受到的浮力,求出水面升高值是本题的突破点.

练习册系列答案
相关题目
 在课外小组活动中,小刚将一挂在弹簧测力计下的形状不规则的物块分别浸没在水和盐水中,弹簧测力计的示数如图所示,物块在水中所受的浮力为
在课外小组活动中,小刚将一挂在弹簧测力计下的形状不规则的物块分别浸没在水和盐水中,弹簧测力计的示数如图所示,物块在水中所受的浮力为 (2005?武汉)在课外小组活动中,小刚将一挂在弹簧测力计下的形状不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示,石块在水中所受到的浮力为
(2005?武汉)在课外小组活动中,小刚将一挂在弹簧测力计下的形状不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示,石块在水中所受到的浮力为 在课外小组活动中,小群用弹簧测力计、形状不规则的系有细线的石块、烧杯、水及盐水分别做了如图所示的实验.由实验可知,石块的质量是
在课外小组活动中,小群用弹簧测力计、形状不规则的系有细线的石块、烧杯、水及盐水分别做了如图所示的实验.由实验可知,石块的质量是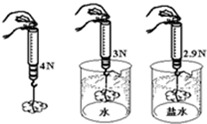 在课外小组活动中,小刚将一挂在弹簧测力计下的形状不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示,石块在水中所受的浮力为
在课外小组活动中,小刚将一挂在弹簧测力计下的形状不规则的石块分别浸没在水和盐水中,弹簧测力计的示数如图所示,石块在水中所受的浮力为