题目内容
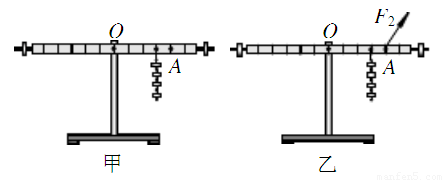
 如图所示杠杆,O为支点.A端挂一质量为5Kg的物体,OA=20cm,OB=12cm,BC=16cm,AO与OB垂直,OB与BC垂直.则在C点需要最小的力为多在才能使之平衡?并画出此力的示意图,作出该杠杆的两个力臂.
如图所示杠杆,O为支点.A端挂一质量为5Kg的物体,OA=20cm,OB=12cm,BC=16cm,AO与OB垂直,OB与BC垂直.则在C点需要最小的力为多在才能使之平衡?并画出此力的示意图,作出该杠杆的两个力臂.分析:根据杠杆平衡的条件,F1L1=F2L2,在杠杆中的阻力、阻力臂一定的情况下,要使所用的动力最小,必须使动力臂最长.而在通常情况下,连接杠杆中支点和动力作用点这两点所得到的线段最长,利用题目中所知数据可计算出力的大小.
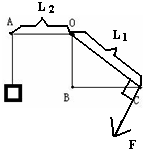
解答:解:(1)连接OC就是最长的动力臂,根据杠杆平衡的条件,要使杠杆平衡动力方向向下,据此可画出最小的动力;如图:
②OC=
=
=20cm,
∴拉力F=
×mg=
×5kg×9.8N=49N.
答:该力的大小为49N,力臂作图如上图所示.

②OC=
| (OB)2+(BC)2 |
| (12cm)2+(16cm)2 |
∴拉力F=
| OA |
| OC |
| 20cm |
| 20cm |
答:该力的大小为49N,力臂作图如上图所示.
点评:要做出杠杆中的最小动力,可以按照以下几个步骤进行:
①确定杠杆中的支点和动力作用点的位置;
②连接支点与动力作用点,得到最长的线段;
③经过动力作用点做出与该线段垂直的直线;
④根据杠杆平衡原理,确定出使杠杆平衡的动力方向.
①确定杠杆中的支点和动力作用点的位置;
②连接支点与动力作用点,得到最长的线段;
③经过动力作用点做出与该线段垂直的直线;
④根据杠杆平衡原理,确定出使杠杆平衡的动力方向.

练习册系列答案
相关题目
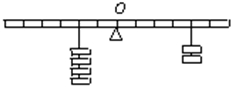 如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是
如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是 如图所示,一均匀木条可绕转轴O自由转动,现有材料相同,长度相同,横截面积之比Sa:Sb:Sc=1:4:2的三支蜡烛a、b、c,垂直立于木条上,木条恰好处于平衡.三支蜡烛离转轴的距离分别为L1、L2和L3,若L1=4L2,则L3=
如图所示,一均匀木条可绕转轴O自由转动,现有材料相同,长度相同,横截面积之比Sa:Sb:Sc=1:4:2的三支蜡烛a、b、c,垂直立于木条上,木条恰好处于平衡.三支蜡烛离转轴的距离分别为L1、L2和L3,若L1=4L2,则L3= 如图所示为“探究杠杆平衡条件”的实验装置.
如图所示为“探究杠杆平衡条件”的实验装置.