题目内容
 如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是
如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是C
C
.A.两边各加一个钩码
B.两边钩码各向外移动一格
C.左边增加一个钩码,右边向外移动一格
D.左右两边的钩码各减少一个
在研究杠杆平衡条件的实验中,总是使杠杆在
水平
水平
位置平衡,这是为了测量力臂
力臂
简便.在实验最初调节杠杆平衡时,发现杠杆右端高,这时应调节平衡螺母
平衡螺母
使它向右
右
移动,直到杠杆平衡.随后在支点两边挂上钩码以后,若杠杆右端下沉,为使杠杆平衡应将钩码
钩码
向左
左
移动.分析:(1)根据杠杆平衡条件:动力×动力臂=阻力×阻力臂来解答此题,力臂可以以格为单位,假设每个钩码的重力为G,一格的长度为L.
(2)杠杆在水平位置平衡,好处有二:一是杠杆的重心在支点上,二是两边支点到力的悬挂点距离为力臂,便于力臂的测量;
杠杆平衡调节原则是:右低将平衡螺母左调,左低将平衡螺母右调;
实验时右低将钩码左移,左低将钩码右移.
(2)杠杆在水平位置平衡,好处有二:一是杠杆的重心在支点上,二是两边支点到力的悬挂点距离为力臂,便于力臂的测量;
杠杆平衡调节原则是:右低将平衡螺母左调,左低将平衡螺母右调;
实验时右低将钩码左移,左低将钩码右移.
解答:解:(1)A、两边各加一个钩码,则左边为5G×2L=1,右边为3G×4L=12,左、右两端力与力臂乘积不等,故不能平衡;
B、两边钩码各向外移动一格,则左边为4G×3L=12,右边为2G×5L=10,左、右两端力与力臂乘积不等,故不能平衡;
C、左边增加一个钩码,右边向外移动一格,则左边为5G×2L=10,右边为2G×5L=10,左、右两端力与力臂乘积相等,故仍能平衡;
D、左右两边的钩码各减少一个,则左边为3G×2L=6,右边为1G×4L=4,左、右两端力与力臂乘积不等,故不能平衡.
(2)杠杆在水平位置平衡,所有的拉力均竖直向下,力臂为支点到力的作用点的距离,以便于力臂的测量;
杠杆右端高,说明水平时重心在支点左边,所以应将平衡螺母右调,使重心右移,杠杆才能平衡;
在支点两边挂上钩码以后,若杠杆右端下沉,说明右边的力与力臂的乘积偏大,将左端的钩码左移,使左边的力与力臂的乘积增大,或将右边的钩码左移,是右边的力与力臂的乘积减小,才能使杠杆平衡.
故答案为:C;水平;力臂;平衡螺母;右;钩码;左.
B、两边钩码各向外移动一格,则左边为4G×3L=12,右边为2G×5L=10,左、右两端力与力臂乘积不等,故不能平衡;
C、左边增加一个钩码,右边向外移动一格,则左边为5G×2L=10,右边为2G×5L=10,左、右两端力与力臂乘积相等,故仍能平衡;
D、左右两边的钩码各减少一个,则左边为3G×2L=6,右边为1G×4L=4,左、右两端力与力臂乘积不等,故不能平衡.
(2)杠杆在水平位置平衡,所有的拉力均竖直向下,力臂为支点到力的作用点的距离,以便于力臂的测量;
杠杆右端高,说明水平时重心在支点左边,所以应将平衡螺母右调,使重心右移,杠杆才能平衡;
在支点两边挂上钩码以后,若杠杆右端下沉,说明右边的力与力臂的乘积偏大,将左端的钩码左移,使左边的力与力臂的乘积增大,或将右边的钩码左移,是右边的力与力臂的乘积减小,才能使杠杆平衡.
故答案为:C;水平;力臂;平衡螺母;右;钩码;左.
点评:(1)该题考查了应用杠杆平衡条件判断杠杆是否平衡,只要分别计算出左、右两边的力与力臂的乘积,看是否相等即可判断.
(2)调节杠杆在水平位置平衡和天平的横梁平衡是相同的,都是调节两端的平衡螺母,并且平衡螺母向上翘的一端移动.
(2)调节杠杆在水平位置平衡和天平的横梁平衡是相同的,都是调节两端的平衡螺母,并且平衡螺母向上翘的一端移动.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目

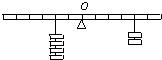
 如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是( )
如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是( ) 如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是( )
如图所示,把一根均匀的米尺,在中点O支起,两端各挂四个钩码和两个钩码,恰好使米尺平衡,按下列方式增减钩码或移动钩码,下列几种方式仍能保持米尺平衡的是( )