题目内容
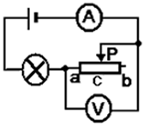 如图所示,电源电压不变,滑动变阻器的滑片P放在c处,已知ac的电阻值为滑动变阻器的总电阻的
如图所示,电源电压不变,滑动变阻器的滑片P放在c处,已知ac的电阻值为滑动变阻器的总电阻的| 1 | 3 |
分析:由电路图可知,灯泡与滑动变阻器串联,电压表测滑动变阻器两端的电压,电流表测电路中的电流.
(1)滑片P放在c处时,根据欧姆定律求出滑动变阻器接入电路中的电阻,进一步求出滑动变阻器的最大阻值,根据电阻的串联和欧姆定律表示出电源的电压;
(2)滑片P放在b处时,根据欧姆定律求出此时电路中的电流,根据电阻的串联和欧姆定律表示出电源的电压,利用电源的电压不变求出灯泡的电阻,根据P=I2R求出两种情况下灯泡的功率.
(1)滑片P放在c处时,根据欧姆定律求出滑动变阻器接入电路中的电阻,进一步求出滑动变阻器的最大阻值,根据电阻的串联和欧姆定律表示出电源的电压;
(2)滑片P放在b处时,根据欧姆定律求出此时电路中的电流,根据电阻的串联和欧姆定律表示出电源的电压,利用电源的电压不变求出灯泡的电阻,根据P=I2R求出两种情况下灯泡的功率.
解答:解:由电路图可知,灯泡与滑动变阻器串联,电压表测滑动变阻器两端的电压,电流表测电路中的电流.
(1)滑片P放在c处时,由I=
可得,滑动变阻器接入电路中的电阻:
Rc=
=
=6Ω,
∵ac的电阻值为滑动变阻器的总电阻的
,
∴滑动变阻器的最大阻值:
Rb=3Rc=3×6Ω=18Ω,
∵串联电路中总电阻等于各分电阻之和,
∴电源的电压:
U=Ic(RL+Rc)=1A×(RL+6Ω);
(2)滑片P放在b处时,电路中的电流:
Ib=
=
=0.5A,
电源的电压:
U=Ib(RL+Rb)=0.5A×(RL+18Ω),
∵电源的电压不变,
∴1A×(RL+6Ω)=0.5A×(RL+18Ω),
解得:RL=6Ω,
则两种情况下灯泡的功率:
PLc=(Ic)2RL=(1A)2×6Ω=6W,PLb=(Ib)2RL=(0.5A)2×6Ω=1.5W.
答:在这两种情况下,灯泡L的功率各为6W、1.5W.
(1)滑片P放在c处时,由I=
| U |
| R |
Rc=
| Uc |
| Ic |
| 6V |
| 1A |
∵ac的电阻值为滑动变阻器的总电阻的
| 1 |
| 3 |
∴滑动变阻器的最大阻值:
Rb=3Rc=3×6Ω=18Ω,
∵串联电路中总电阻等于各分电阻之和,
∴电源的电压:
U=Ic(RL+Rc)=1A×(RL+6Ω);
(2)滑片P放在b处时,电路中的电流:
Ib=
| Ub |
| Rb |
| 9V |
| 18Ω |
电源的电压:
U=Ib(RL+Rb)=0.5A×(RL+18Ω),
∵电源的电压不变,
∴1A×(RL+6Ω)=0.5A×(RL+18Ω),
解得:RL=6Ω,
则两种情况下灯泡的功率:
PLc=(Ic)2RL=(1A)2×6Ω=6W,PLb=(Ib)2RL=(0.5A)2×6Ω=1.5W.
答:在这两种情况下,灯泡L的功率各为6W、1.5W.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活应用,利用好电源的电压不变是关键.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
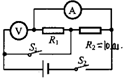 如图所示,电源电压不变,当开关S1、S2同时闭合时,电流表的示数是0.3A,电压表的示数是6V,R1
如图所示,电源电压不变,当开关S1、S2同时闭合时,电流表的示数是0.3A,电压表的示数是6V,R1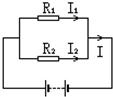 如图所示,电源电压不变,R1=40Ω,R2=20Ω,I1=0.2A.
如图所示,电源电压不变,R1=40Ω,R2=20Ω,I1=0.2A.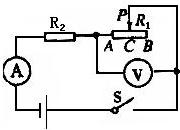 如图所示,电源电压不变,当开关S闭合后,滑动变阻器滑片P在B端时,电压表示数为9V,电流表示数为0.15 A;滑片P在中点C时电压表的示数为6V.
如图所示,电源电压不变,当开关S闭合后,滑动变阻器滑片P在B端时,电压表示数为9V,电流表示数为0.15 A;滑片P在中点C时电压表的示数为6V.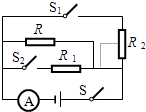
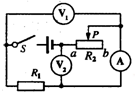 如图所示,电源电压不变,闭合开关S后,滑动变阻器滑片自a向b移动时,电压表V1的示数
如图所示,电源电压不变,闭合开关S后,滑动变阻器滑片自a向b移动时,电压表V1的示数