Question

【题目】一底面积为S0的圆柱形容器中装有适量的水，（水的密度用ρ0表示）质量分别为m1和m2的甲、乙两个实心小球用一根无弹性线连在一起，将他们放入水中后恰好悬浮，如图所示，此时细线上的拉力为T0。

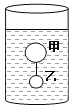
求：（1）甲球的体积

（2）乙球的密度

（3）将细线剪断待小球静止后，水对容器底部压强的变化量Δp

Answer 1

【答案】（1）；（2）（3）

【解析】

根据题中“甲、乙两个实心小球用一根无弹性线连在一起，将他们放入水中后恰好悬浮，求……”可知，本题考查阿基米德原理、密度公式和液体压强的计算。根据图中甲球受力平衡，利用阿基米德原理即可求出甲球的体积。根据图中乙球受力平衡，利用阿基米德原理即可求出乙球的体积，然后利用密度公式求出乙球的密度。把细线剪断后，根据阿基米德原理即可求出受到的总浮力的变化量，即可根据F浮＝ρ水gV排求出排开水的体积减小量，利用V＝Sh求出下降的高度，根据p=ρgh求得水对容器底部压强的变化量。

（1）由图可知：甲球浸没在水中受力平衡，即：F浮1＝G甲+T0，则：ρ0gV甲＝m1g+T0，

所以，甲球的体积

（2）由图可知：乙球浸没在水中受力平衡，即：G乙＝F浮2+T0，则：m2g＝ρ0gV乙+T0，

所以，乙球的体积

，

则乙球的密度

（3）甲、乙两实心小球用一根无弹性细线连在一起在水中后悬浮，则F浮总＝G甲+G乙，

如把细线剪断后，甲球上浮，乙球下沉；则F浮甲＝G甲，F浮乙＝ρ0gV乙，

所以，F浮总′＝F浮甲+F浮乙＝G甲+ρ0gV乙，

△F浮＝F浮总﹣F浮总′＝（G甲+G乙）﹣（G甲+ρ0gV乙）＝G乙﹣ρ0gV乙＝m2g﹣ρ0g×＝，

由F浮＝ρ0gV排可知排开的水的体积减小量为，

所以，水面下降的高度，

水对容器底部压强的变化量