题目内容
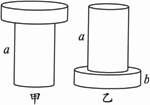
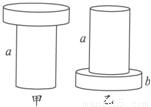
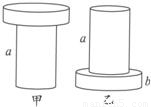
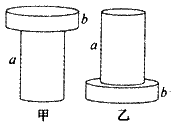
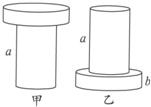如图所示，两个用同种材料制成的圆柱体a和b，b的横截面积是a的3倍，将a竖直放在水平地面上，b竖直放在a上，如图甲所示，这时a对地面的压强与b对a的压强之比为3：2；若a、b倒置后仍放在水平地面上，如图乙所示，则a对b的压强与b对水平地面的压强之比是（ ）| A、1：1 | B、1：2 | C、1：3 | D、1：4 |
分析：在水平地面上，压力等于物体重．
设圆柱体a、b的横截面积为sa、sb，高为ha、hb，可求出圆柱体a、b的重；
则甲图中b对a的压力等于b的重，a对地面的压力等于a和b的总重；乙图中a对b的压力等于a的重，b对地面的压力等于a和b的总重；
又知道受力面积的大小关系，根据压强公式分析判断．
设圆柱体a、b的横截面积为sa、sb，高为ha、hb，可求出圆柱体a、b的重；
则甲图中b对a的压力等于b的重，a对地面的压力等于a和b的总重；乙图中a对b的压力等于a的重，b对地面的压力等于a和b的总重；
又知道受力面积的大小关系，根据压强公式分析判断．
解答：解：设圆柱体a、b的横截面积为sa、sb，高为ha、hb，
则圆柱体a、b的重：Ga=ρgsaha，Gb=ρgsbhb，
在甲图中：
a对地面的压强：p1=
=
，
b对a的压强：p2=
=
，
∵p1：p2=3：2，
∴
：
=3：2；
即：
：
=3：2，
解得：ha：hb=3：2，
设ha=3，hb=2，sa=1，sb=3，
在乙图中：
a对b的压强：p1′=
=
，
b对地面的压强：p2′=
=
，
∴p1′：p2′=
：
=
：
=
：
=1：1．
故选A．
则圆柱体a、b的重：Ga=ρgsaha，Gb=ρgsbhb，
在甲图中：
a对地面的压强：p1=
| F1 |
| sa |
| Ga+Gb |
| sa |
b对a的压强：p2=
| F2 |
| sa |
| Gb |
| sa |
∵p1：p2=3：2，
∴
| Ga+Gb |
| sa |
| Gb |
| sa |
即：
| ρgsaha+ρgsbhb |
| sa |
| ρgsbhb |
| sa |
解得：ha：hb=3：2，
设ha=3，hb=2，sa=1，sb=3，
在乙图中：
a对b的压强：p1′=
| F′1 |
| sa |
| Ga |
| sa |
b对地面的压强：p2′=
| F′2 |
| sb |
| Ga+Gb |
| sb |
∴p1′：p2′=
| Ga |
| sa |
| Ga+Gb |
| sb |
| ρgsaha |
| sa |
| ρgsaha+ρgsbhb |
| sb |
| 1×3 |
| 1 |
| 1×3+3×2 |
| 3 |
故选A．
点评：本题考查了压力和压强的计算，知道在水平地面上，压力等于物体重；确定受力面积的大小是本题的关键．
练习册系列答案
作业辅导系列答案
相关题目
