题目内容
【题目】在综合实践活动中，科技小组设计了一个由压敏电阻控制的报警电路。如图所示，电源电压恒为18V，电阻箱最大阻值为999.9Ω。报警器（电阻不计）通过的电流达到或超过10mA会报警，超过20mA会损坏。压敏电阻Rx在压力不超过800N的前提下，其阻值随压力F的变化规律如下表所示。
压力 F/N | 0 | 50 | 100 | 150 | 200 | 250 | 300 | … |
电阻 Rx/Ω | 580 | 560 | 540 | 520 | 500 | 4.80 | 460 | … |
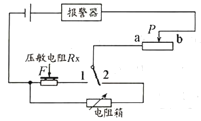
（1）为不损坏元件，报警电路允许消耗的最大功率是多少______？
（2）在压敏电阻Rx所受压力不超过800N的前提下，报警电路所选滑动变阻器的最大阻值不得小于多少______？
（3）现要求压敏电阻受到的压力达到或超过200N时，电路报警。按照下列步骤调试此报警电路：
①电路接通前，滑动变阻器滑片P置于b端；根据实验要求，应将电阻箱调到一定的阻值，这一阻值为_______ Ω；
②将开关向_______端（填数字）闭合，调节_______，直至_______；
③保持_______，将开关向另一端闭合，报警电路即可正常使用。
（4）对（3）中已调试好的报警电路，现要求压敏电阻受到的压力达到或超过700N时，电路报警。若电源电压可调，其它条件不变，则将电源电压调为_______ V即可。
【答案】0.36W 1540Ω 500 2 滑动变阻器的滑片P 报警器报警 滑动变阻器的滑片P位置不变 16
【解析】
(1)超过20mA会损坏，消耗的最大功率是：
；
(2)由表格数据可知，压力每增大50N，电阻R的阻值减小20Ω，即电阻R的阻值随压力F的增大而减小，应是一次函数关系，设为R=kF+b，把F=0N、R=580Ω和F=50N、R=560Ω代入可得：R=580Ω，560Ω=k×50N+b，解得：k=0.4Ω/N，b=580Ω，所以电子元件的阻值R随压力F变化的关系式是R=580Ω0.4Ω/N×F，当压敏电阻Rx所受压力是800N时，电阻为：R=580Ω0.4Ω/N×800N，解得：R=260N，当电路中的电流为10mA时，电路中的总电阻：
，则此时滑动变阻器的最大阻值：R′=R总R=1800Ω260Ω=1540Ω；
(3)现要求压敏电阻受到的压力达到或超过200N时，电路报警。按照下列步骤调试此报警电路：
①电路接通前，滑动变阻器滑片P置于b端；根据实验要求，应将电阻箱调到一定的阻值，这一阻值为500Ω，要求压敏电阻受到的压力达到或超过200N时，由表中数据可得，此时压敏电阻是500Ω；
②为了保证电阻箱电阻500Ω连入电路，将开关向2端闭合，调节滑动变阻器的滑片P，直至报警器报警，这时滑动变阻器的一部分电阻也连入电路；
③利用控制变量法，保持滑动变阻器的滑片P位置不变，即滑动变阻器的电阻不变，将开关向1端闭合，报警电路即可正常使用，即保证压力达到或超过200N时，电路报警；
(4)压敏电阻是500Ω时，滑动变阻器的电阻：
，压敏电阻受到的压力达到或超过700N时，由R=580Ω0.4Ω/N×F，得电阻是：R=300Ω，电路报警时需要的电源电压：
.
阅读快车系列答案
【题目】如图所示，有一柱状的薄透明玻璃容器(在它的外面有表示高度的刻度纸)和一底面积是20cm2高8cm并刻有高度的圆柱体(密度大于水的密度，用细线系着)。某实验小阻利用这两个器材探究：当物体浸入柱状容器的水中时，水对容器底增大的压强与水对物体的浮力之间有什么关系。
他们先往容器中加水至10.00cm刻度处（图中己标出）)，再用细线吊圆柱体，让圆柱体浸入水中的深度h先后是:2.00cm，4.00cm，6.00cm、8.00cm，读出容器底到水面对应增加深度△h，利用阿基米德原理公式和液体压强公式分别计算出对应的浮力F浮和水对容器底增加的压强△p，结果如下表
F浮/N | 0.4 | 0.8 | 1.2 | 1.6 |
Δp/Pa | 100 | 200 | 300 | 400 |
(1)分析表中数据可知，当圆柱体浸入柱状容器的水中时，水对容器底增大的压强与水对物体的浮力成________，如果物体浸没后继续增大它在水中的深度，F浮和△p都________（选填“增大”或“不变”或“减小”)；
(2)同学们又从另一个角度讨论了这种关系的成因：当物体浸入水中时，水对物体施加了竖直向上的浮力，由于________________物体对水也会施加大小相等的竖直向下的压力，使容器底部增大的压力大小为F浮(柱状容器底面积为S)，那么△p=________(用所给物理量字母表示)；
(3)根据本次实验数据，计算出容器底面积S=________cm2，因此圆柱体浸没在水中时，水面所对的刻度是________cm。
