题目内容
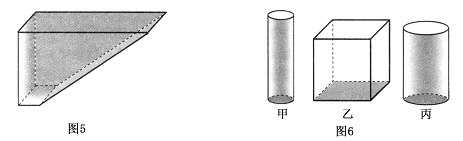
【题目】在水平地面上并排铺有![]() 块相同的均质砖块,如图甲,每块砖的质量为m,长为a,宽为b,厚为c。若要将这n块砖按图乙所示叠放在最左边的砖块上,则至少要给砖块做的功
块相同的均质砖块,如图甲,每块砖的质量为m,长为a,宽为b,厚为c。若要将这n块砖按图乙所示叠放在最左边的砖块上,则至少要给砖块做的功

A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】A
【解析】因为将地面上的砖块叠放,使每一块砖提升的高度不同,所做的功也不同,所以首先需要利用W=Gh分别求出对每一块砖所做的功,即:
第一块砖提升高度为:h1 =0,第二块砖提升高度为:h2 =c,第三块砖提升高度为:h3 =2c,…第n块砖提升高度是:hn =(n-1)c,
所以对第一块砖所做的功是:W1 =Gh1 =mg×0=0,对第二块砖所做的功是:W2 =Gh2 =mg×c=mgc,对第三块砖所做的功是:W3 =G3 =mg×2c=2mgc,…对第n块砖所做的功是:Wn =Gn =mg×(n-1)c=(n-1)mgc,
故整个过程做的功是:W总 =W1 +W2 +W3 +…+Wn=0+mgc+mg2c+…+(n-1)mgc=〔1+2+…+(n-1)〕mgc=n(n1)/2mgc,故选A。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目