题目内容
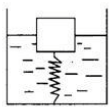 如图所示,一根弹簧原长15厘米,其下端固定在容器底部,上端连接一个边长为4厘米的正方体实心木块,向容器里注水,当水深达到18厘米时,木块一半浸入水中;当水深达到22厘米时,木块上表面正好与水面相平,求木块的密度.
如图所示,一根弹簧原长15厘米,其下端固定在容器底部,上端连接一个边长为4厘米的正方体实心木块,向容器里注水,当水深达到18厘米时,木块一半浸入水中;当水深达到22厘米时,木块上表面正好与水面相平,求木块的密度.分析:已知木块的边长,可求木块的体积,根据阿基米德原理可求木块全部浸没后受到的浮力,从而求出浸没一半时受到的浮力,求出此时弹簧的伸长量;再求出当水深达到22厘米时,最后分析木块的受力,根据二力平衡求出木块的密度.
解答:解:当木块全部浸没时受到的浮力F浮全=ρ水gV排=1.0×103kg/m3×10N/kg×(0.04m)3=0.64N;
木块一半浸入水中,受到的浮力F浮半=
F浮=
×0.64N=0.32N;
当水深达到18厘米时,弹簧的伸长量为L1=18cm-2cm-15cm=1cm;
当水深达到22厘米时,弹簧的伸长量为L2=22cm-4cm-15cm=3cm;
当水深达到18厘米和22厘米时,木块都受到竖直向下的重力G、弹簧的拉力F和竖直向上的浮力F浮的作用,木块受力平衡,所以G+F=F浮,所以F=F浮-G;
水深分别达到18厘米和22厘米时,浮力增加了△F浮=F浮全-F浮半=0.64N-0.32N=0.32N;
∴拉力增加了△F=△F浮=0.32N;
∴弹簧伸长2厘米是受到的拉力为0.32N;
∴当水深达到18厘米时,拉力F1=
×1cm=0.16N,
∴G=F浮半-F1=0.32N-0.16N=0.16N,
∴木块的质量m=
=
=0.016kg,
∴木块的密度ρ木=
=
=0.25×103kg/m3.
答:木块的密度为0.25×103kg/m3.
木块一半浸入水中,受到的浮力F浮半=
| 1 |
| 2 |
| 1 |
| 2 |
当水深达到18厘米时,弹簧的伸长量为L1=18cm-2cm-15cm=1cm;
当水深达到22厘米时,弹簧的伸长量为L2=22cm-4cm-15cm=3cm;
当水深达到18厘米和22厘米时,木块都受到竖直向下的重力G、弹簧的拉力F和竖直向上的浮力F浮的作用,木块受力平衡,所以G+F=F浮,所以F=F浮-G;
水深分别达到18厘米和22厘米时,浮力增加了△F浮=F浮全-F浮半=0.64N-0.32N=0.32N;
∴拉力增加了△F=△F浮=0.32N;
∴弹簧伸长2厘米是受到的拉力为0.32N;
∴当水深达到18厘米时,拉力F1=
| 0.32N |
| 2cm |
∴G=F浮半-F1=0.32N-0.16N=0.16N,
∴木块的质量m=
| G |
| g |
| 0.16N |
| 10N/kg |
∴木块的密度ρ木=
| m |
| V |
| 0.016kg |
| (0.04m)3 |
答:木块的密度为0.25×103kg/m3.
点评:本题考查密度的计算,难点是根据弹簧的伸长量求出拉力的大小,从而进一步求出木块的重力,本题难度较大,解题时一定要认真仔细.

练习册系列答案
相关题目
为制作弹簧测力计,某物理实验小组对弹簧的伸长与拉力的关系作了探究.下表是他们利用甲、乙两根不同的弹簧做实验时所记录的数据.
表一:
|
甲弹簧受到的拉力/N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
甲弹簧的长度/cm |
6.0 |
9.0 |
12.0 |
15.0 |
18.0 |
21.0 |
24.0 |
表二:
|
乙弹簧受到的拉力/N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
乙弹簧的长度/cm |
6.0 |
7.5 |
9.0 |
10.5 |
12.0 |
13.5 |
15.0 |
(1)分析表一和表二数据可知:①_______________。
②在拉力相同的情况下,甲弹簧伸长的长度比乙弹簧大___(选填“大“或“小”).
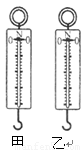
(2)分别使用甲、乙两弹簧制成如图所示的甲、乙两弹簧测力计,它们的外壳相同,刻度线分布情况相同,则量程较大的是___(选填“甲”或“乙”下同)测力计,精度较高的是___测力计.
(3)经实验探究发现:在拉力相同的情况下,弹簧伸长的长度与弹簧的材料、粗细、原长(弹簧不受外力时的长度)等均有关系,请设计一个简单实验,证实弹簧伸长的长度与弹簧原长有关。
 (1)分析表一和表二数据可知:
(1)分析表一和表二数据可知: (2012?徐汇区二模)为了研究弹簧受到拉力时,影响其长度增加量的有关因素,小明同学用测力计及一些不同的弹簧进行实验.如图所示,在实验中小明分别用力通过测力计拉伸不同的弹簧,测量并记录每根弹簧的原长、弹簧圈直径、长度增加量、所受拉力的大小等.记录数据如下列各表格所示,已知在同一表格中,实验所用弹簧的材料相同(即相同粗细的同种金属丝).
(2012?徐汇区二模)为了研究弹簧受到拉力时,影响其长度增加量的有关因素,小明同学用测力计及一些不同的弹簧进行实验.如图所示,在实验中小明分别用力通过测力计拉伸不同的弹簧,测量并记录每根弹簧的原长、弹簧圈直径、长度增加量、所受拉力的大小等.记录数据如下列各表格所示,已知在同一表格中,实验所用弹簧的材料相同(即相同粗细的同种金属丝).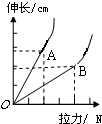 某同学用一根弹簧制作弹簧测力计的实验时,在弹簧的下端挂不同重力的钩码,对应弹簧的长度也不同,具体数据见下表:
某同学用一根弹簧制作弹簧测力计的实验时,在弹簧的下端挂不同重力的钩码,对应弹簧的长度也不同,具体数据见下表: