题目内容
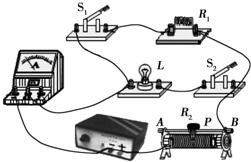 (2011?东城区一模)如图所示的电路中,电源电压不变,定值电阻R1=25Ω,滑动变阻器R2的最大阻值为15Ω,灯泡L上标有“6V 4W”字样,不考虑灯丝电阻随温度的变化,电流表量程为0~0.6A,当只闭合S1,滑动变阻器滑片P在B端时,电流表的示数为0.2A.当只闭合S2时,要求灯L两端的电压不超过额定电压,电流表的示数不超过此量程,调节滑动变阻器滑片P,灯泡L功率的变化范围是
(2011?东城区一模)如图所示的电路中,电源电压不变,定值电阻R1=25Ω,滑动变阻器R2的最大阻值为15Ω,灯泡L上标有“6V 4W”字样,不考虑灯丝电阻随温度的变化,电流表量程为0~0.6A,当只闭合S1,滑动变阻器滑片P在B端时,电流表的示数为0.2A.当只闭合S2时,要求灯L两端的电压不超过额定电压,电流表的示数不超过此量程,调节滑动变阻器滑片P,灯泡L功率的变化范围是1~3.24
1~3.24
W.分析:当只闭合S1,电阻R1与滑动变阻器的最大阻值R2串联,电流表测电路中电流,根据串联电路电阻特点和欧姆定律求出电源的电压;
当只闭合S2时,灯泡L与滑动变阻器串联,先根据R=
求出灯泡的电阻,再根据I=
求出灯泡的额定电流与电流表的量程相比较,得出电路的最大电流;由欧姆定律可知当滑动变阻器接入电路的电阻最大时,电路中电流最小,利用电阻的串联特点和欧姆定律进一步求出,最后利用P=I2R分别求出灯泡的最大和最小电功率即可求出答案.
当只闭合S2时,灯泡L与滑动变阻器串联,先根据R=
| U2 |
| P |
| P |
| U |
解答:解:当只闭合S1,电阻R1与滑动变阻器的最大阻值R2串联,
电源的电压为U=I(R1+R2)=0.2A×(25Ω+15Ω)=8V;
当只闭合S2时,灯泡L与滑动变阻器串联,
灯泡的电阻为RL=
=
=9Ω
灯泡的额定电流为I额=
=
≈0.67A>0.6A,
所以此时电路的最大电流I最大=0.6A,
此时灯泡的实际功率最大为P最大=(I最大)2RL=(0.6A)2×9Ω=3.24W;
当滑动变阻器接入电路的电阻最大时,电路中的电流最小为
I最小=
=
=
A,
此时灯泡的实际功率最小为P最小=(I最小)2RL=(
A)2×9Ω=1W;
所以灯泡L功率的变化范围是1~3.24W.
故答案为:1~3.24W.
电源的电压为U=I(R1+R2)=0.2A×(25Ω+15Ω)=8V;
当只闭合S2时,灯泡L与滑动变阻器串联,
灯泡的电阻为RL=
| ||
| P额 |
| (6V)2 |
| 4W |
灯泡的额定电流为I额=
| P额 |
| U额 |
| 4W |
| 6V |
所以此时电路的最大电流I最大=0.6A,
此时灯泡的实际功率最大为P最大=(I最大)2RL=(0.6A)2×9Ω=3.24W;
当滑动变阻器接入电路的电阻最大时,电路中的电流最小为
I最小=
| U |
| RL+R2 |
| 8V |
| 9Ω+15Ω |
| 1 |
| 3 |
此时灯泡的实际功率最小为P最小=(I最小)2RL=(
| 1 |
| 3 |
所以灯泡L功率的变化范围是1~3.24W.
故答案为:1~3.24W.
点评:本题考查了串联电路的特点和欧姆定率、电功率的计算,关键是开关闭合和断开时电路串并联的辨别,难点是灯泡最大和最小实际电流的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
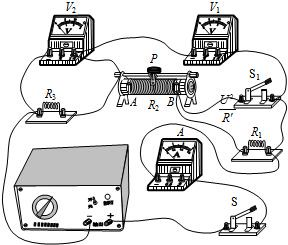 (2011?东城区一模)如图所示的电路中,电源两端的电压保持不变.闭合开关S、S1,当滑片P移至滑动变阻器R2的A端时,电压表V1的示数为U1,电压表V2的示数为U2,电流表A的示数为I1,滑动变阻器R2消耗的电功率P2为3W.当只闭合开关S,将滑片P移至滑动变阻器R2的中点时,电压表V1的示数为U1′,电压表V2的示数为U2′,电流表A的示数为I2.闭合开关S、S1,当滑片P移至滑动变阻器R2的B端时,电流表A的示数为I3,电阻R3的电功率为P3.
(2011?东城区一模)如图所示的电路中,电源两端的电压保持不变.闭合开关S、S1,当滑片P移至滑动变阻器R2的A端时,电压表V1的示数为U1,电压表V2的示数为U2,电流表A的示数为I1,滑动变阻器R2消耗的电功率P2为3W.当只闭合开关S,将滑片P移至滑动变阻器R2的中点时,电压表V1的示数为U1′,电压表V2的示数为U2′,电流表A的示数为I2.闭合开关S、S1,当滑片P移至滑动变阻器R2的B端时,电流表A的示数为I3,电阻R3的电功率为P3.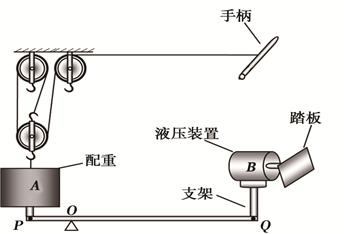 (2011?东城区一模)如图所示是某种健身器械的示意图,轻质支架固定在轻质杠杆PQ两端,O为支点,PO:OQ=1:4.液压装置B可使支架获得与作用在踏板上的力大小相同、竖直向下的压力,配重A重GA=1500N悬挂在滑轮组下方,其下表面与支架接触,动滑轮重G动=100N.人对滑轮轴处手柄施水平向右的拉力F=200N时,杠杆恰在水平位置平衡.为加大训练强度,将支点移至O′处,PO′:O′Q=1:1,人对手柄施水平向右的拉力F1,同时对踏板施压力N1,配重A以v=0.2m/s的速度竖直向上略微提升,杠杆P端匀速略微竖直向上抬起,这时滑轮组的机械效率为η1.继续加大训练强度,增加的配重为GA′,同时移动支点至O″处,PO″:O″Q=4:1,人对手柄施水平向右的拉力F2,此时对踏板施压力N2,配重被竖直向上匀速的略微提升,杠杆P端被匀速略微竖直向上抬起,这时滑轮组的机械效率为η2.滑轮组的绳重、绳的伸长和轮轴间摩擦可以忽略,F:F1:F2=1:2:3,N1:N2=3:11.
(2011?东城区一模)如图所示是某种健身器械的示意图,轻质支架固定在轻质杠杆PQ两端,O为支点,PO:OQ=1:4.液压装置B可使支架获得与作用在踏板上的力大小相同、竖直向下的压力,配重A重GA=1500N悬挂在滑轮组下方,其下表面与支架接触,动滑轮重G动=100N.人对滑轮轴处手柄施水平向右的拉力F=200N时,杠杆恰在水平位置平衡.为加大训练强度,将支点移至O′处,PO′:O′Q=1:1,人对手柄施水平向右的拉力F1,同时对踏板施压力N1,配重A以v=0.2m/s的速度竖直向上略微提升,杠杆P端匀速略微竖直向上抬起,这时滑轮组的机械效率为η1.继续加大训练强度,增加的配重为GA′,同时移动支点至O″处,PO″:O″Q=4:1,人对手柄施水平向右的拉力F2,此时对踏板施压力N2,配重被竖直向上匀速的略微提升,杠杆P端被匀速略微竖直向上抬起,这时滑轮组的机械效率为η2.滑轮组的绳重、绳的伸长和轮轴间摩擦可以忽略,F:F1:F2=1:2:3,N1:N2=3:11.