题目内容
 在图所示的装置中,质量可忽略不计的杠杆CD可绕转轴O点自由转动,OC:OD=2:1,A、B两个滑轮的质量均为2kg,E是边长为20cm、密度为ρ1的正方体合金块,合金块E通过滑轮A用轻细线悬吊着全部浸没在密度为ρ2的液体中.当质量为60kg的人用F1=75N的力竖直向下拉绳时,杠杆恰好在水平位置平衡,此时人对地面的压强为p1=1.05×104Pa;若把密度为ρ2的液体换成密度为ρ3的液体,合金块E全部浸没在密度为ρ3的液体中,人用F2的力竖直向下拉绳,杠杆在水平位置平衡,此时人对地面的压强为p2=1.034×104Pa.若ρ2:ρ3=5:4,取g=10N/kg,人与地面接触的面积保持不变,杠杆和滑轮的摩擦均可忽略不计,求:
在图所示的装置中,质量可忽略不计的杠杆CD可绕转轴O点自由转动,OC:OD=2:1,A、B两个滑轮的质量均为2kg,E是边长为20cm、密度为ρ1的正方体合金块,合金块E通过滑轮A用轻细线悬吊着全部浸没在密度为ρ2的液体中.当质量为60kg的人用F1=75N的力竖直向下拉绳时,杠杆恰好在水平位置平衡,此时人对地面的压强为p1=1.05×104Pa;若把密度为ρ2的液体换成密度为ρ3的液体,合金块E全部浸没在密度为ρ3的液体中,人用F2的力竖直向下拉绳,杠杆在水平位置平衡,此时人对地面的压强为p2=1.034×104Pa.若ρ2:ρ3=5:4,取g=10N/kg,人与地面接触的面积保持不变,杠杆和滑轮的摩擦均可忽略不计,求:(1)人用F1拉绳时,杠杆C端所受的拉力大小;
(2)F2的大小;
(3)合金块E的密度ρ1.
分析:(1)对于滑轮B,除受到重力外,还受到两段绳子的拉力,由此得到杠杆C端受到的拉力;
(2)由于第一次人对地面的压力、压强已知,可以得到双脚与地面的接触面积;已知第二次对地面的压强和双脚与地面的接触面积,得到拉力F2的大小;
(3)①已知两种情况下,人对绳子的拉力,利用杠杆的平衡条件可以得到两种情况下绳子对合金块的拉力;
②合金块浸没在液体中受到三个力的作用:重力、拉力和浮力,利用三者的等量关系列出方程组,求解合金块的密度.
(2)由于第一次人对地面的压力、压强已知,可以得到双脚与地面的接触面积;已知第二次对地面的压强和双脚与地面的接触面积,得到拉力F2的大小;
(3)①已知两种情况下,人对绳子的拉力,利用杠杆的平衡条件可以得到两种情况下绳子对合金块的拉力;
②合金块浸没在液体中受到三个力的作用:重力、拉力和浮力,利用三者的等量关系列出方程组,求解合金块的密度.
解答:已知:mA=mB=2kg g=10N/kg F1=75N m人=60kg p1=1.05×104Pa p2=1.034×104Pa
=
求:(1)TC1=?(2)F2=?(3)ρ1=?
解:
(1)两个滑轮受到的重力为GA=GB=mBg=2kg×10N/kg=20N,
人用F1拉绳时,杠杆C端所受的拉力大小
TC1=2F1+GB=75N×2+20N=170N;
(2)人受到的重力为G人=m人g=60kg×10N/kg=600N,
∵p=
,
∴p1=
=
=
=1.05×104Pa,
解得S=0.05m2,
∵p2=
,
∴F2=G人-p2S=600N-1.034×104Pa×0.05m2=83N;
(3)①设合金块E全部浸没在密度为ρ2的液体中时绳对其拉力为T1,对于人用F1=75N的力拉绳时,
根据杠杆平衡条件有OC?(2F1+GB)=OD?(2T1+GA)
即2×170N=2T1+20N,
解得T1=160N;
同理,设合金块E全部浸没在密度为ρ3的液体中时绳对其拉力为T2,则有
OC?(2F2+GB)=OD?(2T2+GA)
即2×(2×83N+20N)=2T2+20N,
解得T2=176N;
②对于合金块E全部浸没时,根据平衡条件则有G=F浮+T,即T=(ρ1-ρ液)gV
所以合金块E全部浸没在密度为ρ2的液体中时有T1=G-F浮1=ρ1gV-ρ2gV=(ρ1-ρ2)gV
即160N=(ρ1-ρ2)gV ①
同理,合金块E全部浸没在密度为ρ3的液体中时有T2=(ρ1-ρ3)gV
即176N=(ρ1-ρ3)gV ②
又因
=
③,
联立上述几式,并代入数据解得ρ1=3×103kg/m3.
答:(1)人用F1拉绳时,杠杆C端所受的拉力为170N;
(2)F2为83N;
(3)合金块E的密度ρ1为3×103kg/m3.
| ρ2 |
| ρ3 |
| 5 |
| 4 |
求:(1)TC1=?(2)F2=?(3)ρ1=?
解:
(1)两个滑轮受到的重力为GA=GB=mBg=2kg×10N/kg=20N,
人用F1拉绳时,杠杆C端所受的拉力大小
TC1=2F1+GB=75N×2+20N=170N;
(2)人受到的重力为G人=m人g=60kg×10N/kg=600N,
∵p=
| F |
| S |
∴p1=
| G人-F1 |
| S |
| 600N-75N |
| S |
| 525N |
| S |
解得S=0.05m2,
∵p2=
| G人-F2 |
| S |
∴F2=G人-p2S=600N-1.034×104Pa×0.05m2=83N;
(3)①设合金块E全部浸没在密度为ρ2的液体中时绳对其拉力为T1,对于人用F1=75N的力拉绳时,
根据杠杆平衡条件有OC?(2F1+GB)=OD?(2T1+GA)
即2×170N=2T1+20N,
解得T1=160N;
同理,设合金块E全部浸没在密度为ρ3的液体中时绳对其拉力为T2,则有
OC?(2F2+GB)=OD?(2T2+GA)
即2×(2×83N+20N)=2T2+20N,
解得T2=176N;
②对于合金块E全部浸没时,根据平衡条件则有G=F浮+T,即T=(ρ1-ρ液)gV
所以合金块E全部浸没在密度为ρ2的液体中时有T1=G-F浮1=ρ1gV-ρ2gV=(ρ1-ρ2)gV
即160N=(ρ1-ρ2)gV ①
同理,合金块E全部浸没在密度为ρ3的液体中时有T2=(ρ1-ρ3)gV
即176N=(ρ1-ρ3)gV ②
又因
| ρ2 |
| ρ3 |
| 5 |
| 4 |
联立上述几式,并代入数据解得ρ1=3×103kg/m3.
答:(1)人用F1拉绳时,杠杆C端所受的拉力为170N;
(2)F2为83N;
(3)合金块E的密度ρ1为3×103kg/m3.
点评:此题是一道力学综合题,涉及到杠杆平衡条件、力的作用的相互性、阿基米德原理、重力的计算和压强计算公式的应用,对物体进行正确的受力分析,在头脑中确定正确的等量关系,是解决此类难题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 (2010?宣武区二模)如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求:
(2010?宣武区二模)如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求: (2012?丹东)某剧组为拍摄需要,设计了如图所示的装置来改变照明灯的高度.轻质杠杆ABO可绕O点转动,在图中画出ABO所受阻力F2的示意图,并画出动力臂L1和阻力臂L2.
(2012?丹东)某剧组为拍摄需要,设计了如图所示的装置来改变照明灯的高度.轻质杠杆ABO可绕O点转动,在图中画出ABO所受阻力F2的示意图,并画出动力臂L1和阻力臂L2.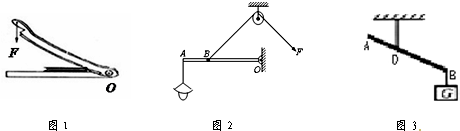
 过去几百年来许多人一直致力于发明一种永动机,包括伟大的科学家牛顿,但都以失败告终.近几年来,科学家发现某种合金具有“形状记忆功能”:如果在较低温度时将它弯曲成某一形状,然后加热到较高温度时再弯曲成另一形状,那么当降低到原来较低温度时,它就会自行恢复到低温时的形状.现用它制成如图所示的装置:在可绕圆心O转动的均匀轻质圆盘上,安装一个用形状记忆合金做成的螺旋圈,它们在温度低时收紧、温度高时放松.实验表明:当把该圆盘的下半部分浸在盛有一定量热水的水槽中时,只要给圆盘一个起始转动的力,圆盘就能克服摩擦和水的阻力连续转动起来.这不就是一个可以不消耗能量的“永动机”吗?
过去几百年来许多人一直致力于发明一种永动机,包括伟大的科学家牛顿,但都以失败告终.近几年来,科学家发现某种合金具有“形状记忆功能”:如果在较低温度时将它弯曲成某一形状,然后加热到较高温度时再弯曲成另一形状,那么当降低到原来较低温度时,它就会自行恢复到低温时的形状.现用它制成如图所示的装置:在可绕圆心O转动的均匀轻质圆盘上,安装一个用形状记忆合金做成的螺旋圈,它们在温度低时收紧、温度高时放松.实验表明:当把该圆盘的下半部分浸在盛有一定量热水的水槽中时,只要给圆盘一个起始转动的力,圆盘就能克服摩擦和水的阻力连续转动起来.这不就是一个可以不消耗能量的“永动机”吗? 小丽同学利用如图所示的装置,将系在细线上的轻质小球靠近音叉来探究“声音的强弱与什么因素有关”.实验中通过改变施力的大小来改变声源的振幅.
小丽同学利用如图所示的装置,将系在细线上的轻质小球靠近音叉来探究“声音的强弱与什么因素有关”.实验中通过改变施力的大小来改变声源的振幅.