题目内容
【题目】如图所示,两个底面积不同的圆柱形容器内分别盛有深度不同的液体,已知距容器底部均为h的A、B两点的压强相等.现将实心金属球甲、乙分别浸没在左右两液体中,均无液体溢出,此时A点的压强大于B点的压强,则一定成立的是( ) 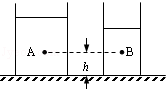
A.甲球的质量小于乙球的质量
B.甲球的质量大于乙球的质量
C.甲球的体积小于乙球的体积
D.甲球的体积大于乙球的体积
【答案】D
【解析】解:设A点到液面的距离是hA , B点到液面的距离是hB , 由图知:hA>hB , 因为A、B两点的压强相等,由P=ρgh,得:ρAghA=ρBghB , ρAhA=ρBhB , 因为hA>hB , 所以ρA<ρB ,
金属球甲、乙分别浸没在A、B两液体中,设液面上升的高度分别为:△hA、△hB , A点的压强大于B点的压强,
即:ρAg(hA+△hA)>ρBg(h'B+△hB),因为ρAhA=ρBhB , ρA<ρB , 所以△hA>△hB ,
由图知两容器的底面积SA>SB , 两球浸没在液体中,液面上升的体积,即两球排开液体的体积SA△hA>SB△hB ,
因为两球排开液体的体积等于它们自身的体积,所以V甲>V乙 , 球的质量m=ρV,因为不知道两球的密度关系,
所以不能判断两球的质量关系.
故选D.
根据图找出A、B两点到液面的距离关系,两容器的底面积关系;
由A、B两点压强相等,由液体压强公式判断出两液体的密度关系;
因为甲、乙两球浸没在液体中A点压强大于B点压强,再根据液体压强公式判断出甲乙两球的体积关系;
最后根据公式m=ρV判断两球的质量关系.

练习册系列答案
相关题目


