题目内容
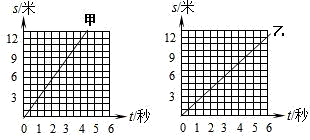 P,Q是同一直线上相距12米的两点,甲从P点向Q方向、乙从Q点同时沿直线同向而行,它们运的 s-t 图象如图所示,分析图象可知
P,Q是同一直线上相距12米的两点,甲从P点向Q方向、乙从Q点同时沿直线同向而行,它们运的 s-t 图象如图所示,分析图象可知
- A.甲的速度小于乙的速度
- B.经过3秒,甲、乙相距3米
- C.甲、乙相遇时离Q点6米
- D.甲到达Q点时,乙离P点20米
D
分析:A、甲和乙路程、时间的图象都是一条过原点的直线,说明了甲和乙都是做匀速直线运动的,分别找出甲和乙运动1s的路程,再根据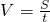 求出甲和乙的运动速度进行比较;
求出甲和乙的运动速度进行比较;
B、根据S=Vt求出甲和乙三秒运动的路程,再根据甲和乙原来的距离进行计算;
C、甲和乙是同时出发的,相遇时甲和乙运动的时间是相等的,距离Q点的距离也是相等的,乙是从Q点出发的,根据S=Vt就是乙运动的路程就行,乙的速度在A中已经计算出来了,运动的时间可以根据V甲t-V乙t=12m求出;
D、甲从P点出发,运动到Q点,运动的路程是12m,根据 求出甲的运动时间;相同的时间内,根据S=Vt求出乙运动的路程,乙是从Q点出发的,原来相距P点的距离12m,加上运动的路程就行.
求出甲的运动时间;相同的时间内,根据S=Vt求出乙运动的路程,乙是从Q点出发的,原来相距P点的距离12m,加上运动的路程就行.
解答:A、甲和乙的运动图象都是一条过原点的直线,说明甲和乙都是做匀速直线运动的;甲在1s的时间内运动的距离是3m,速度 ,乙在1s的时间内运动的距离是2m,速度
,乙在1s的时间内运动的距离是2m,速度 ,所以甲的速度大于乙的速度;
,所以甲的速度大于乙的速度;
B、经过3s,甲的运动路程S甲=V甲t=3m/s×3s=9m,乙的运动路程S乙=V乙t=2m/s×3s=6m,甲比乙多运动了3m;原来甲和乙相距12m,现在甲赶上了3m,甲和乙此时相距12m-3m=9m;
C、设甲、乙从开始到相距的时间为t,则V甲t-V乙t=12m,代入数据得到3m/s×t-2m/s×t=12m,解方程得知t=12s;甲和乙相遇时,它们到Q点的距离是相等的,乙从Q点出发,运动的路程S乙=V乙t=2m/s×12s=24m,所以甲和乙相距Q点的距离为24m;
D、甲到达Q点,甲是从P点出发的,甲的运动路程为12m,运动的时间 ;乙和甲是同时出发的,乙的运动时间和甲的运动时间是相同的,乙的运动路程S乙=V乙t=2m/s×4s=8m,乙是从Q点开始出发的,Q点距P点12m,乙又运动了8m,所以乙距离P点是12m+8m=20m.
;乙和甲是同时出发的,乙的运动时间和甲的运动时间是相同的,乙的运动路程S乙=V乙t=2m/s×4s=8m,乙是从Q点开始出发的,Q点距P点12m,乙又运动了8m,所以乙距离P点是12m+8m=20m.
故选D.
点评:此题考查的是我们对于图象的分析能力和速度公式的灵活应用,需要我们认真的分析才能做出正确的解答.
分析:A、甲和乙路程、时间的图象都是一条过原点的直线,说明了甲和乙都是做匀速直线运动的,分别找出甲和乙运动1s的路程,再根据
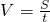 求出甲和乙的运动速度进行比较;
求出甲和乙的运动速度进行比较;B、根据S=Vt求出甲和乙三秒运动的路程,再根据甲和乙原来的距离进行计算;
C、甲和乙是同时出发的,相遇时甲和乙运动的时间是相等的,距离Q点的距离也是相等的,乙是从Q点出发的,根据S=Vt就是乙运动的路程就行,乙的速度在A中已经计算出来了,运动的时间可以根据V甲t-V乙t=12m求出;
D、甲从P点出发,运动到Q点,运动的路程是12m,根据
 求出甲的运动时间;相同的时间内,根据S=Vt求出乙运动的路程,乙是从Q点出发的,原来相距P点的距离12m,加上运动的路程就行.
求出甲的运动时间;相同的时间内,根据S=Vt求出乙运动的路程,乙是从Q点出发的,原来相距P点的距离12m,加上运动的路程就行.解答:A、甲和乙的运动图象都是一条过原点的直线,说明甲和乙都是做匀速直线运动的;甲在1s的时间内运动的距离是3m,速度
 ,乙在1s的时间内运动的距离是2m,速度
,乙在1s的时间内运动的距离是2m,速度 ,所以甲的速度大于乙的速度;
,所以甲的速度大于乙的速度;B、经过3s,甲的运动路程S甲=V甲t=3m/s×3s=9m,乙的运动路程S乙=V乙t=2m/s×3s=6m,甲比乙多运动了3m;原来甲和乙相距12m,现在甲赶上了3m,甲和乙此时相距12m-3m=9m;
C、设甲、乙从开始到相距的时间为t,则V甲t-V乙t=12m,代入数据得到3m/s×t-2m/s×t=12m,解方程得知t=12s;甲和乙相遇时,它们到Q点的距离是相等的,乙从Q点出发,运动的路程S乙=V乙t=2m/s×12s=24m,所以甲和乙相距Q点的距离为24m;
D、甲到达Q点,甲是从P点出发的,甲的运动路程为12m,运动的时间
 ;乙和甲是同时出发的,乙的运动时间和甲的运动时间是相同的,乙的运动路程S乙=V乙t=2m/s×4s=8m,乙是从Q点开始出发的,Q点距P点12m,乙又运动了8m,所以乙距离P点是12m+8m=20m.
;乙和甲是同时出发的,乙的运动时间和甲的运动时间是相同的,乙的运动路程S乙=V乙t=2m/s×4s=8m,乙是从Q点开始出发的,Q点距P点12m,乙又运动了8m,所以乙距离P点是12m+8m=20m.故选D.
点评:此题考查的是我们对于图象的分析能力和速度公式的灵活应用,需要我们认真的分析才能做出正确的解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
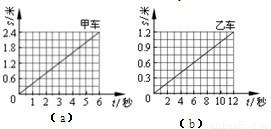
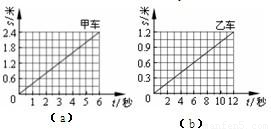
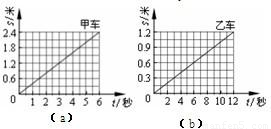
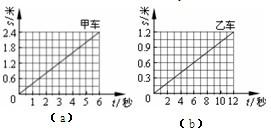 (2012?黄陂区模拟)P、Q 是同一直线上相距 1.2 米的两点,甲从 P 点、乙从 Q 点同时沿直线相向而行,它们运动的 s-t 图象如图 (a)、(b)所示,分析图象可知( )
(2012?黄陂区模拟)P、Q 是同一直线上相距 1.2 米的两点,甲从 P 点、乙从 Q 点同时沿直线相向而行,它们运动的 s-t 图象如图 (a)、(b)所示,分析图象可知( )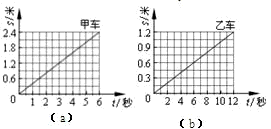 P、Q 是同一直线上相距 1.2 米的两点,甲从 P 点、乙从 Q 点同时沿直线相向而行,它们运动的 s-t 图象如图 (a)、(b)所示,分析图象可知
P、Q 是同一直线上相距 1.2 米的两点,甲从 P 点、乙从 Q 点同时沿直线相向而行,它们运动的 s-t 图象如图 (a)、(b)所示,分析图象可知