题目内容
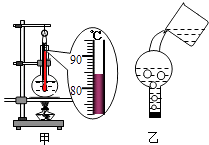
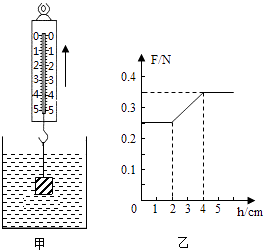
【题目】( 2014来宾)如图甲所示,在容器底部固定一轻质弹簧,弹簧上端连有一边长为0.1m的正方体物块A,当容器中水的深度为20cm时,物块A有 ![]() 的体积露出水面,此时弹簧恰好处于自然伸长状态(ρ水=1.0×103kg/m3 , g取10N/kg).求:
的体积露出水面,此时弹簧恰好处于自然伸长状态(ρ水=1.0×103kg/m3 , g取10N/kg).求: 
(1)物块A受到的浮力;
(2)物块A的密度;
(3)往容器缓慢加水(水未溢出)至物块A恰好浸没时水对容器底部压强的增加量△p(整个过程中弹簧受到的拉力跟弹簧的伸长量关系如图乙所示).
【答案】
(1)物块A体积为V=(0.1m)3=0.001m3,
则V排=V﹣V露=V﹣ ![]() V=
V= ![]() V=
V= ![]() ×0.001m3=6×10﹣4m3,
×0.001m3=6×10﹣4m3,
∴F浮=ρ水gV排=1×103kg/m3×10N/kg×6×10﹣4m3=6N
答:物块A受到的浮力为6N
(2)弹簧恰好处于自然状态时没有发生形变
F浮=G,
ρ水gV排=ρ物gV,
ρ物= ![]() ρ水=
ρ水= ![]() ×1×103kg/m3=0.6×103kg/m3
×1×103kg/m3=0.6×103kg/m3
答:物块A的密度为0.6×103kg/m3
(3)物块A刚好完全浸没水中
F1=F浮﹣G=ρ水gV﹣ρ物gV=1×103kg/m3×10N/kg×10﹣3m3﹣0.6×103kg/m3×10N/kg×10﹣3m3=4N;
由图乙可知:此时弹簧伸长了4cm,
当容器中水的深度为20cm时,物块A有 ![]() 的体积露出水面,此时弹簧恰好处于自然伸长状态,
的体积露出水面,此时弹簧恰好处于自然伸长状态,
则弹簧原长L0=h水﹣hA浸=20cm﹣(1﹣ ![]() )×10cm=14cm,
)×10cm=14cm,
∴物块A刚好完全浸没水中弹簧长度L′=L0+△L=14cm+4cm=18cm;
则水面的高度为h2=L′+LA=18cm+10cm=28cm,
∴水面升高的高度△h=h2﹣h水=28cm﹣20cm=8cm=0.08m.
△p=ρ水g△h=1×103kg/m3×10N/kg×0.08m=800Pa.
答:往容器缓慢加水(水未溢出)至物块A恰好浸没时水对容器底部压强的增加量△p为800Pa
【解析】(1)根据物体边长和物块A体积露出水面的比例,求出排开水的体积,根据公式F浮=ρ水gV排求出浮力.(2)利用物体的沉浮条件,此时物块漂浮.F浮=G,根据公式ρ水gV排=ρ物gV求出木块的密度;(3)因物块A刚好完全浸没水中,此时弹簧对物块A的作用力为F=F浮﹣G,求出F,由图乙可知弹簧的伸长量,因物块A恰好浸没时,由此可知水面升高的高度根据液体压强公式P=ρgh求出水对容器底部压强的增加量.
【考点精析】解答此题的关键在于理解密度的计算的相关知识,掌握密度公式:ρ = m/v,以及对液体的压强的计算的理解,了解液体内部压强的公式:p=ρgh ρ指密度,单位kg/m3,g=9.8N/kg, h指深度,单位:m,压强单位(Pa) 注意:h 指液体的深度,即某点到液面的距离.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案