题目内容
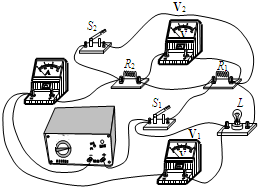 (2013?东城区一模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化.当只闭合开关S1时,电流表的示数是I1.当只闭合开关S2时,电流表的示数是I2.当开关S1、S2都闭合时,灯L正常发光,电流表的示数为I3.当开关S1、S2都断开时,电流表的示数是I4,电压表V1、V2示数之比为3:1,此时RL消耗的电功率为0.5W;已知I1:I2=3:1,求:
(2013?东城区一模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化.当只闭合开关S1时,电流表的示数是I1.当只闭合开关S2时,电流表的示数是I2.当开关S1、S2都闭合时,灯L正常发光,电流表的示数为I3.当开关S1、S2都断开时,电流表的示数是I4,电压表V1、V2示数之比为3:1,此时RL消耗的电功率为0.5W;已知I1:I2=3:1,求:(1)电阻R1:R2;
(2)电流I3:I4;
(3)电路总功率的最大值Pm.
分析:先画出四种情况的等效电路图.
(1)根据欧姆定律分别表述出图①和图②中的电源,利用电源的电压不变结合两图的电流关系即可得出R2与RL的电阻关系,根据串联电路的电流特点和欧姆定律表示出图④中两电压表的示数即可两示数关系即可得出 R1与R2的比值;
(2)根据并联电路的电压特点和欧姆定律表示出各支路的电流,利用并联电路的电流特点表示出图③中干路电流,利用电阻的串联特点和欧姆定律表示出图④中电流,结合灯泡与两电阻的阻值关系即可求出I3:I4;
(3)灯泡与两电阻并联时电路总功率最大,根据电阻的并联特点表示出图③中的总电阻,根据P=I2R表示出图④中灯泡的实际功率和图③中的总功率,然后两者相比即可求出电路总功率的最大值Pm.
(1)根据欧姆定律分别表述出图①和图②中的电源,利用电源的电压不变结合两图的电流关系即可得出R2与RL的电阻关系,根据串联电路的电流特点和欧姆定律表示出图④中两电压表的示数即可两示数关系即可得出 R1与R2的比值;
(2)根据并联电路的电压特点和欧姆定律表示出各支路的电流,利用并联电路的电流特点表示出图③中干路电流,利用电阻的串联特点和欧姆定律表示出图④中电流,结合灯泡与两电阻的阻值关系即可求出I3:I4;
(3)灯泡与两电阻并联时电路总功率最大,根据电阻的并联特点表示出图③中的总电阻,根据P=I2R表示出图④中灯泡的实际功率和图③中的总功率,然后两者相比即可求出电路总功率的最大值Pm.
解答:解:S1闭合,等效电路图如图①所示;
S2闭合,等效电路图如图②所示;
S1、S2闭合,等效电路图如图③所示;
S1、S2断开,等效电路图如图④所示.
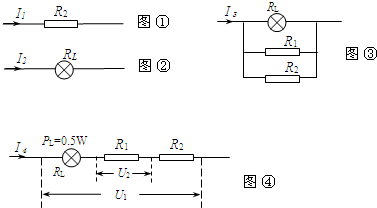
(1)图①和图②中
∵电源的电压不变,
∴根据欧姆定律可得:
=
=
,
图④中
∵串联电路中各处的电流相等,
∴
=
=
=
=
解得:
=
;
(2)图③中
∵并联电路中各支路两端的电压相等,且干路电流等于各支路电流之和,
∴I3=
+
+
=
+
+
=
,
图④中
I4=
=
=
,
∴
=
=
;
(3)并联时总功率最大,
由图④可得,电路中的总电阻:
∵并联电路中总电阻的倒数等于各支路电阻到数之和,
∴
=
+
+
=
+
+
=
,
∴R并=
=
×
=
,
=(
)2×
=(
)2×
=
,
解得Pm=22PL=22×0.5W=11W.
答:(1)电阻R1:R2为2:1;
(2)电流I3:I4为11:1;
(3)电路总功率的最大值为11W.
S2闭合,等效电路图如图②所示;
S1、S2闭合,等效电路图如图③所示;
S1、S2断开,等效电路图如图④所示.

(1)图①和图②中
∵电源的电压不变,
∴根据欧姆定律可得:
| I1 |
| I2 |
| RL |
| R2 |
| 3 |
| 1 |
图④中
∵串联电路中各处的电流相等,
∴
| U1 |
| U2 |
| RL+R1+R2 |
| R1 |
| 3R2+R1+R2 |
| R1 |
| 4R2+R1 |
| R1 |
| 3 |
| 1 |
解得:
| R1 |
| R2 |
| 2 |
| 1 |
(2)图③中
∵并联电路中各支路两端的电压相等,且干路电流等于各支路电流之和,
∴I3=
| U |
| RL |
| U |
| R1 |
| U |
| R2 |
| U |
| 3R2 |
| U |
| 2R2 |
| U |
| R2 |
| 11U |
| 6R2 |
图④中
I4=
| U |
| RL+R1+R2 |
| U |
| 3R2+2R2+R2 |
| U |
| 6R2 |
∴
| I3 |
| I4 |
| ||
|
| 11 |
| 1 |
(3)并联时总功率最大,
由图④可得,电路中的总电阻:
∵并联电路中总电阻的倒数等于各支路电阻到数之和,
∴
| 1 |
| R并 |
| 1 |
| RL |
| 1 |
| R1 |
| 1 |
| R2 |
| 1 |
| 3R2 |
| 1 |
| 2R2 |
| 1 |
| R2 |
| 11 |
| 6R2 |
∴R并=
| 6R2 |
| 11 |
| 6 |
| 11 |
| RL |
| 3 |
| 2RL |
| 11 |
| pm |
| pL |
| I3 |
| I4 |
| R并 |
| RL |
| 11 |
| 1 |
| 2 |
| 11 |
| 22 |
| 1 |
解得Pm=22PL=22×0.5W=11W.
答:(1)电阻R1:R2为2:1;
(2)电流I3:I4为11:1;
(3)电路总功率的最大值为11W.
点评:本题考查了串联电路的特点和并联电路的特点以及欧姆定律、电功率公式的灵活应用,画出四中情况下的等效电路图和利用好电流关系、电压关系是关键.

练习册系列答案
相关题目
 (2013?东城区一模)在如图所示的装置内,分别用两个试管给10g水和10g油加热,其温度随时间变化的关系图象如图所示,水的比热容是4.2×103J/(kg?℃),则( )
(2013?东城区一模)在如图所示的装置内,分别用两个试管给10g水和10g油加热,其温度随时间变化的关系图象如图所示,水的比热容是4.2×103J/(kg?℃),则( ) (2013?东城区一模)在如图所示电路中,电源电压保持不变,闭合开关S,电压表V1的示数用U1表示,电压表V2的示数用U2表示,电流表A的示数用I表示,定值电阻和滑动变阻器的阻值分别用R1、R2表示.当滑动变阻器的滑片P向右移动时,下列说法一定正确的是( )
(2013?东城区一模)在如图所示电路中,电源电压保持不变,闭合开关S,电压表V1的示数用U1表示,电压表V2的示数用U2表示,电流表A的示数用I表示,定值电阻和滑动变阻器的阻值分别用R1、R2表示.当滑动变阻器的滑片P向右移动时,下列说法一定正确的是( )