题目内容
小明去某古镇旅游时发现,米酒是当地的一种特产.小店卖米酒和卖酱油都用竹筒状的容器来量取,但量取相同质量的米酒和酱油时,所选用的器具是不一样的,如图1所示.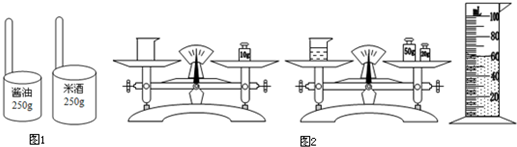
(1)请你用学过的物理知识对“使用不同容器”这种现象进行解释.
(2)小明在古镇买了一瓶米酒,回家后,按照如图2所示的过程进行了实验,测出了米酒的密度.由图所示的数据可知米酒的密度为
(3)按照小明的实验方案测出来的米酒密度偏大还是偏小?请你写出改进方案.

(1)请你用学过的物理知识对“使用不同容器”这种现象进行解释.
(2)小明在古镇买了一瓶米酒,回家后,按照如图2所示的过程进行了实验,测出了米酒的密度.由图所示的数据可知米酒的密度为
1.0×103
1.0×103
kg/m3.(3)按照小明的实验方案测出来的米酒密度偏大还是偏小?请你写出改进方案.
分析:(1)根据密度的公式可知,当质量相同时,密度越大的物体,其体积会越小;
(2)由图中天平和量筒分别读出质量和体积的示数,利用密度公式ρ=
计算即可;
(3)这种测量方法结果使测得液体体积偏小了,因为有一部分液体滞留在烧杯中,测得密度就偏大了.
(2)由图中天平和量筒分别读出质量和体积的示数,利用密度公式ρ=
| m |
| V |
(3)这种测量方法结果使测得液体体积偏小了,因为有一部分液体滞留在烧杯中,测得密度就偏大了.
解答:解:(1)因为酱油和米酒的密度不同,如果选用相同大小的容器,则相同的体积下酱油和米酒的质量不相等,因此要用不同体积的容器.
(2)由图中天平和量筒读出质量m=(50g+20g)-10g=60g,体积V=60cm3,
∴米酒的密度为:ρ=
=
=1.0g/cm3=1.0×103kg/m3.
(3)小明先测空烧杯的质量,再测烧杯和米酒的总质量,再将烧杯中的米酒倒入量筒中测出其体积,因为有一部分米酒滞留在烧杯中,所以测得米酒的体积偏小了,所以测得的米酒的密度偏大;为了减小误差可先测烧杯和米酒的总质量,再将烧杯中的米酒倒入量筒中测出其体积,再测出剩余的米酒和烧杯的质量,即按B→C→A的顺序进行实验.
故答案为:
(1)因为酱油和米酒的密度不同,如果选用相同大小的容器,则相同的体积下酱油和米酒的质量不相等,因此要用不同体积的容器;
(2)1.0×103;
(3)量筒中的时候,米酒无法全部倒出,导致测出的米酒的体积偏小,因此所测米酒的密度偏大;
正确方法:
A.在烧杯中放一些米酒,放到天平上称出烧杯和米酒质量为m1;
B.将烧杯中的米酒倒入量筒中一部分,测出体积V;
C.用天平称出剩余米酒和烧杯的质量为m2;
D.ρ=
.
(2)由图中天平和量筒读出质量m=(50g+20g)-10g=60g,体积V=60cm3,
∴米酒的密度为:ρ=
| m |
| V |
| 60g |
| 60cm3 |
(3)小明先测空烧杯的质量,再测烧杯和米酒的总质量,再将烧杯中的米酒倒入量筒中测出其体积,因为有一部分米酒滞留在烧杯中,所以测得米酒的体积偏小了,所以测得的米酒的密度偏大;为了减小误差可先测烧杯和米酒的总质量,再将烧杯中的米酒倒入量筒中测出其体积,再测出剩余的米酒和烧杯的质量,即按B→C→A的顺序进行实验.
故答案为:
(1)因为酱油和米酒的密度不同,如果选用相同大小的容器,则相同的体积下酱油和米酒的质量不相等,因此要用不同体积的容器;
(2)1.0×103;
(3)量筒中的时候,米酒无法全部倒出,导致测出的米酒的体积偏小,因此所测米酒的密度偏大;
正确方法:
A.在烧杯中放一些米酒,放到天平上称出烧杯和米酒质量为m1;
B.将烧杯中的米酒倒入量筒中一部分,测出体积V;
C.用天平称出剩余米酒和烧杯的质量为m2;
D.ρ=
| m1-m2 |
| V |
点评:本题根据实际生活中的一个例子考查了密度公式的应用及测量液体密度的方法,注意设计实验时要设计合理.

练习册系列答案
相关题目


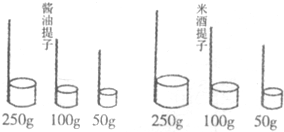 小明去某古镇旅游时发现,米酒是当地的一种特产.小店卖米酒和卖酱油都用竹筒状的容器来量取.但量取相同质量的米酒时所用的器具比量取酱油的要大一点,如图所示.请你利用所学的物理知识对这种现象做出解释.你对次量具有何评价?
小明去某古镇旅游时发现,米酒是当地的一种特产.小店卖米酒和卖酱油都用竹筒状的容器来量取.但量取相同质量的米酒时所用的器具比量取酱油的要大一点,如图所示.请你利用所学的物理知识对这种现象做出解释.你对次量具有何评价?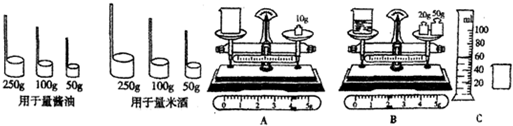
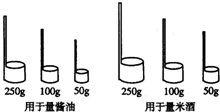 小明去某古镇旅游时发现,米酒是当地的一种特产.小店卖米酒和卖酱油都用竹筒状的容器来量取,但量取相同质量的米酒时所用的器具比量取酱油的要大一点,如图所示.请你利用所学的物理知识判断米酒和酱油密度较大的是
小明去某古镇旅游时发现,米酒是当地的一种特产.小店卖米酒和卖酱油都用竹筒状的容器来量取,但量取相同质量的米酒时所用的器具比量取酱油的要大一点,如图所示.请你利用所学的物理知识判断米酒和酱油密度较大的是