题目内容
【题目】一个质量为3kg、底面积为100 cm2、装有20 cm深的水的圆柱形容器放在水平桌面上,容器的厚度忽略不计。A、B是由密度不同的材料制成的两实心物块,已知A物块的体积是B物块体积的2倍。当把A、B两物块用细线相连放入水中时,两物块恰好悬浮,且没有水溢出,如图所示,现剪断细线,稳定后水对容器底的压强变化了50 Pa,物块A有1/4体积露出水面.下列说法正确的是

A. A物体体积为 50cm3
B. B物体密度为3×103kg/m3
C. 物体A、B放入后,容器对桌面的压强为5.3×103Pa
D. 细线剪断待B静止后,B对容器底的压力为1.4N
【答案】C
【解析】
A. 由p=ρgh可得,细线被剪断后水面高度的减小量:
![]() ,此时物块A有
,此时物块A有![]() 体积露出水面,则A露出水面的体积和容器内减少的体积相等,即
体积露出水面,则A露出水面的体积和容器内减少的体积相等,即![]() ,则物体A的体积:
,则物体A的体积:
VA=4S容△h=4×100cm2×0.5cm=200cm3,故A错误;
B. 细线被剪断后A漂浮,物块A有![]() 体积露出水面,则V排A=
体积露出水面,则V排A=![]() VA,
VA,
因物体漂浮时受到的浮力和自身的重力相等,
所以由F浮=ρgV排和G=mg=ρVg可得:
ρ水gV排A=ρAVAg,则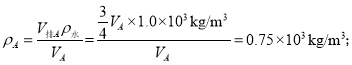
已知A物块的体积是B物块体积的2倍,即VA=2VB,
剪断细线前AB两物块恰好悬浮,则根据F浮=ρgV排、G=mg和ρ=mV可得:
ρ水g(VA+VB)=ρAVAg+ρBVBg,B物体的密度:
![]() ,故B错误;
,故B错误;
C. 圆柱形容器内水的体积:V水=S容h水=100cm2×20cm=2000cm3,
由ρ=mV可得,水的质量:m水=ρ水V水=1.0g/cm3×2000cm3=2000g=2kg,
容器对水平桌面的压力:F容=G总=(m容+m水)g=(3kg+2kg)×10N/kg=50N,
物块A和B的重力之和为:A物块的体积是B物块体积的2倍,则VB=![]() VA=
VA=![]() ×200cm3=100cm3,
×200cm3=100cm3,
A物块的重力为:GA=mAg=ρAVAg=0.75×103kg/m3×200×106m3×10N/kg=1.5N
B物块的重力:GB=mBg=ρBVBg=1. 5×103kg/m3×100×106m3×10N/kg=1.5N,
所以GA+GB=3N;
容器对水平桌面的压强:
![]() ,故C正确;
,故C正确;
D.因为B物块的重力为1.5N,B浸没在水中,则V排B=VB=100cm3,
B物块受到的浮力:F浮B=ρ水gV排B=1×103kg/m3×10N/kg×100×106m3=1N,
所以B对容器底的压力为:F压=GBF浮B=1.5N1N=0.5N.故D错误。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案






