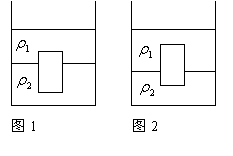题目内容
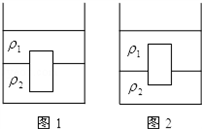
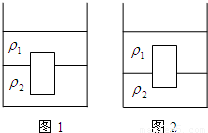
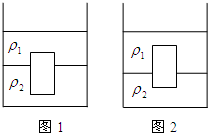如图所示容器中装有两种互不相溶且界限分明的液体，密度分别为ρ1、ρ2将一圆柱体放入容器中，圆柱体的密度为ρ3．静止时圆柱体的上表面到分界线的距离为l1，如图1所示．将第一个圆柱体取出，再将另一形状与体积完全相同，但用不同材料制成的圆柱体放入容器中，静止时圆柱体的上表面到分界线的距离为l2，如图2所示，求后一圆柱体密度．分析：由图1和图2可知，两次的圆柱体在两种液体中悬浮，分别根据物体的浮沉条件和阿基米德原理以及密度公式得出等式，然后进行求解即可得出后一圆柱体密度．
解答：解：设圆柱体的体积为V，高度为l，则
由图1可知，物体悬浮，
所以ρ3Vg=ρ1gV排1+ρ2gV排2，即ρ3Vg=ρ1g
V+ρ2g
V，
l=
l1；
由图2可知，物体悬浮，
所以ρ4Vg=ρ1gV排3+ρ2gV排4，即ρ4Vg=ρ1g
V+ρ2g
V，
把l的值代入上式可得ρ4=
（ρ3-ρ2）+ρ2．
答：后一圆柱体密度为
（ρ3-ρ2）+ρ2．
由图1可知，物体悬浮，
所以ρ3Vg=ρ1gV排1+ρ2gV排2，即ρ3Vg=ρ1g
| l1 |
| l |
| l-l1 |
| l |
l=
| ρ1-ρ2 |
| ρ3-ρ2 |
由图2可知，物体悬浮，
所以ρ4Vg=ρ1gV排3+ρ2gV排4，即ρ4Vg=ρ1g
| l2 |
| l |
| l-l2 |
| l |
把l的值代入上式可得ρ4=
| l2 |
| l1 |
答：后一圆柱体密度为
| l2 |
| l1 |
点评：本题考查了物体浮沉条件、密度公式和阿基米德原理的应用，关键是利用好两圆柱体体积不变这一条件．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
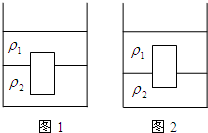如图所示容器中装有两种互不相溶且界限分明的液体，密度分别为ρ1、ρ2将一圆柱体放入容器中，圆柱体的密度为ρ3．静止时圆柱体的上表面到分界线的距离为l1，如图1所示．将第一个圆柱体取出，再将另一形状与体积完全相同，但用不同材料制成的圆柱体放入容器中，静止时圆柱体的上表面到分界线的距离为l2，如图2所示，求后一圆柱体密度．
和
，将一圆柱体放入容器中，圆柱体的密度为
。静止时圆柱体的上表面到分界线的距离为
，如图1所示。将第一个圆柱体取出，再将另一形状与体积完全相同，但用不同材料制成的圆柱体放入容器中，静止时圆柱体的上表面到分界线的距离为
，如图2所示，求后一圆柱体密度。