题目内容
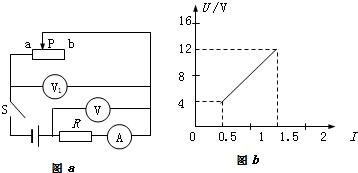
 如图a所示的电路中,电源电压保持不变,闭合开关S后,滑动变阻器的滑片P由a端移动到b端时,测得电阻R两端的电压U与通过电阻R的电流I的变化关系如图b所示.求:
如图a所示的电路中,电源电压保持不变,闭合开关S后,滑动变阻器的滑片P由a端移动到b端时,测得电阻R两端的电压U与通过电阻R的电流I的变化关系如图b所示.求:(1)电源的电压.
(2)变阻器的最大阻值.
(3)当P滑到中点时,通电1min,电路产生的总热量是多少?
(4)通过计算分析变阻器的滑片P由a端移动到b端的过程中,电阻R消耗的电功率变化情况.
分析:(1)滑动变阻器的滑片P在a端时,电路中只有电阻R,电压表V测量R两端的电压,也就是电源电压,电压表V1测量滑动变阻器两端的电压,此时滑动变阻器接入电路电阻为0,示数也就为0,从图象上可以看出电源电压的大小.
(2)滑动变阻器的滑片P由a端移动到b端时,滑动变阻器和电阻串联,此时滑动变阻器接入电路的电阻最大,根据欧姆定律可知,此时电路电流最小,电阻R两端的电压最小,从图象上可以看出R两端的最小电压和最小电流,电源电压不变,根据串联电压的特点,进一步求出滑动变阻器两端的电压,根据欧姆定律求出滑动变阻器的最大阻值.
(3)滑动变阻器的滑片P在中点时,首先根据P滑到b端时,R两端的电压值和电路中的电流值,利用欧姆定律求出定值电阻的阻值,再根据串联电路的电阻规律求出滑片P在中点时总电阻值,根据公式Q=W=
t即可求出.
(4)变阻器滑片P位于a端和b端时,R两端的电压和电流都能从图象上找到,电阻R的功率根据公式P=UI可求.
(2)滑动变阻器的滑片P由a端移动到b端时,滑动变阻器和电阻串联,此时滑动变阻器接入电路的电阻最大,根据欧姆定律可知,此时电路电流最小,电阻R两端的电压最小,从图象上可以看出R两端的最小电压和最小电流,电源电压不变,根据串联电压的特点,进一步求出滑动变阻器两端的电压,根据欧姆定律求出滑动变阻器的最大阻值.
(3)滑动变阻器的滑片P在中点时,首先根据P滑到b端时,R两端的电压值和电路中的电流值,利用欧姆定律求出定值电阻的阻值,再根据串联电路的电阻规律求出滑片P在中点时总电阻值,根据公式Q=W=
| U2 |
| R |
(4)变阻器滑片P位于a端和b端时,R两端的电压和电流都能从图象上找到,电阻R的功率根据公式P=UI可求.
解答:解:(1)由图可知,P滑到a端时,V的示数最大,等于电源电压.即U=12V.
答:电源的电压为12V.
(2)P滑到b端时,R两端的电压为4V,串联电路的电流为0.5A,则:
Rab=
=
=16Ω,
答:变阻器的最大阻值为16Ω.
(3)因为P滑到b端时,R两端的电压为4V,串联电路的电流为0.5A,
所以,R=
=
=8Ω,
当P在中点时,则电路中的总阻值为:
R总=
Rab+R=
×16Ω+8Ω=16Ω,
∴Q=
t=
×60s=540J.
答:通电1min,电路产生的总热量是540J.
(4)由图可知,当P在a端时,UR=12V,Ia=1.5A,
∴Pa=URIa=12V×1.5A=18W;
而当P在b端时,UR=4V,Ib=0.5A,
∴Pb=URIb=4V×0.5A=2W;
故P由a端移动到b端的过程中,电阻R消耗的电功率逐渐变小.
答:变阻器的滑片P由a端移动到b端的过程中,电阻R消耗的电功率有18W变为2W.
答:电源的电压为12V.
(2)P滑到b端时,R两端的电压为4V,串联电路的电流为0.5A,则:
Rab=
| Uab |
| I |
| 12V-4V |
| 0.5A |
答:变阻器的最大阻值为16Ω.
(3)因为P滑到b端时,R两端的电压为4V,串联电路的电流为0.5A,
所以,R=
| U |
| I |
| 4V |
| 0.5A |
当P在中点时,则电路中的总阻值为:
R总=
| 1 |
| 2 |
| 1 |
| 2 |
∴Q=
| U2 |
| R总 |
| (12V)2 |
| 16Ω |
答:通电1min,电路产生的总热量是540J.
(4)由图可知,当P在a端时,UR=12V,Ia=1.5A,
∴Pa=URIa=12V×1.5A=18W;
而当P在b端时,UR=4V,Ib=0.5A,
∴Pb=URIb=4V×0.5A=2W;
故P由a端移动到b端的过程中,电阻R消耗的电功率逐渐变小.
答:变阻器的滑片P由a端移动到b端的过程中,电阻R消耗的电功率有18W变为2W.
点评:本题考查电压、电阻、电热、电功率等的计算,关键是公式及其变形的灵活运用,难点是明白滑片移动过程中电路的变化情况,本题考查了应用图象解决问题,这是以后学习的重点.

练习册系列答案
相关题目
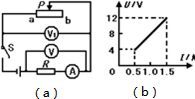 如图a所示的电路中,电源电压保持不变,闭合开关S后,滑动变阻器的滑片P由a端移动到b端时,测得电阻R两端的电压U与通过电阻R的电流I的变化关系如图b所示.求:
如图a所示的电路中,电源电压保持不变,闭合开关S后,滑动变阻器的滑片P由a端移动到b端时,测得电阻R两端的电压U与通过电阻R的电流I的变化关系如图b所示.求: