题目内容
【题目】如图所示,将一个体积为1.0×10﹣3m3、重6N的木块用细线系在底面积为400cm2的圆柱形容器的底部.当容器中倒入足够的水使木块被浸没时,求: 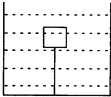
(1)木块浸没在水中受到的浮力?
(2)剪断细线后,木块处于静止时,木块露出水面的体积多大?
(3)木块露出水面处于静止后,容器底部所受水的压强减小了多少?
【答案】
(1)解:木块浸没在水中时受到的浮力:
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.0×10﹣3m3=10N;
(2)解:因为木块浸没在水中时的浮力大于木块的重力,
所以剪断细线后,木块会上浮直至漂浮在水面上,
由于漂浮,所以F浮′=G=6N,
由F浮=ρ水gV排得排开水的体积:
V排′= ![]() =
= ![]() =6×10﹣4m3,
=6×10﹣4m3,
则V露=V﹣V排′=1.0×10﹣3m3﹣6×10﹣4m3=4×10﹣4m3;
(3)解:木块露出水面处于静止后,水面下降的高度:
△h= ![]() =
= ![]() =0.01m,
=0.01m,
则容器底部所受水的压强减小了:△p=ρ水g△h=1.0×103kg/m3×10N/kg×0.01m=100Pa.
【解析】(1)已知木块的体积,则就可以知道它浸没时排开水的体积,那么知道了V排和水的密度,则可以根据阿基米德原理公式就可以算出木块浸没在水中时受到的浮力;(2)由题意可知,剪断细线后,木块时漂浮在水面上的,则F浮=G,知道了木块受到的浮力大小,就可以根据阿基米德原理公式的变形式算出此时木块在水中的V排 , 最后用木块的体积减去V排就算出了木块露出水面的体积;(3)液体压强公式是P=ρ液gh,要算容器底部所受水的压强减小了多少,就需要先算出液面高度下降了多少,而液面下降的高度取决于木块露出水面的体积,所以用木块露出水面的体积除以容器的底面积,就可以算出水面减小的高度,从而就可以算出减小的压强.
【考点精析】根据题目的已知条件,利用液体的压强的计算和阿基米德原理的相关知识可以得到问题的答案,需要掌握液体内部压强的公式:p=ρgh ρ指密度,单位kg/m3,g=9.8N/kg, h指深度,单位:m,压强单位(Pa) 注意:h 指液体的深度,即某点到液面的距离;阿基米德原理:浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开的液体所受的重力.这个规律叫做阿基米德原理,即 F浮= G排 =ρ液gv排.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案

