题目内容
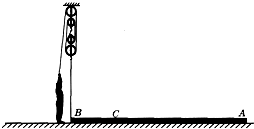（2010?朝阳区一模）一根不均匀的金属杆长AB=4m，自重为G=4 000N，放在水平地面上．如图所示的滑轮组的绳子系在B端，以A端为支点，竖直向上地提起它的B端．当人站在水平地面上，竖直向下用力拉绳端，使金属杆的B端刚离开地面时，人对地面的压力为FN1，B端受到竖直向上的拉力为F1，若匀速略微向上提起金属杆的过程中，滑轮组的绳重、绳的伸长和轮轴问摩擦可以忽略，滑轮组的机械效率保持不变为η1．；当把该滑轮组的绳子系在金属杆的C点，AC=3m，仍以A端为支点，匀速略微竖直向上拉起B端，人对地面的压力为F№时，C点受到竖直向上的拉力为F2，B端恰好离开地面，这时滑轮组的机械效率为η2．若人的体重为G人=700N且保持不变，FNl：FN2=12：7，η1：η2=63：64．求：（1）F1与F2的比值；
（2）动滑轮重G动；
（3）金属杆的重心0距A端的距离．
分析：（1）设金属杆重心0距A端的距离为L2，知道B端受到竖直向上的拉力F1和C点受到竖直向上的拉力为F2，又知道AB和AC的长度，再根据杠杆的平衡条件可以列出两个等式，即F1AB=G杆L2，F2AC=G杆L2，便可以计算出F1与F2的比值①．
（2）滑轮组的绳重、绳的伸长和轮轴问摩擦可以忽略，知道B端受到竖直向上的拉力F1和C点受到竖直向上的拉力为F2，滑轮组在此图情形的机械效率的计算如下：η=
=
=
=
，再借助η1：η2=63：64，从而可以列出一个机械效率比值的等式②．
（3）从图可知，有四段绳子吊着物体，则绳子末端的拉力就等于竖直向上的拉力和动滑轮重力的
，人未离开地面，处于平衡状态，人受到竖直向下的重力、竖直向上的支持力和拉力，人对地面的压力的大小也就是支持力的大小，则人对地面的压力就等于人的重力减去绳子末端的拉力，再借助FNl：FN2=12：7，从而可以列出一个人对地面的压力比值的等式③．
①②③组成方程组便可以计算出出F1、F2和动滑轮重G动．再把F1代入F1AB=G杆L2便可以计算出金属杆的重心0距A端的距离．
（2）滑轮组的绳重、绳的伸长和轮轴问摩擦可以忽略，知道B端受到竖直向上的拉力F1和C点受到竖直向上的拉力为F2，滑轮组在此图情形的机械效率的计算如下：η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额外 |
| F拉力h |
| F拉力h+G动h |
| F拉力 |
| F拉力+G动 |
（3）从图可知，有四段绳子吊着物体，则绳子末端的拉力就等于竖直向上的拉力和动滑轮重力的
| 1 |
| 4 |
①②③组成方程组便可以计算出出F1、F2和动滑轮重G动．再把F1代入F1AB=G杆L2便可以计算出金属杆的重心0距A端的距离．
解答：解：（1）设金属杆重心0距A端的距离为L2，B端受到竖直向上的拉力F1，C点受到竖直向上的拉力为F2，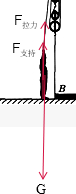
根据杠杆的平衡条件可知：F1AB=G杆L2，F2AC=G杆L2，
则F1AB=F2AC，
∴
=
=
=
①．
（2）∵滑轮组的绳重、绳的伸长和轮轴问摩擦可以忽略，
∴η=
=
=
=
，
即
=
=
×
=
，
化简得：64F1（F2+G动）=63F2（F1+G动），
即：F1F2+64F1G动=63F2G动②．
（3）从图可知，有四段绳子吊着物体，则绳子末端的拉力就等于竖直向上的拉力和动滑轮重力的
，
从图可知，人对地面的压力就等于人的重力减去绳子末端的拉力，
∴
=
=
=
，
化简得：12F2-7F1+5G动=14000N③，
则
=
=
=
①，F1F2+64F1G动=63F2G动②，12F2-7F1+5G动=14000N③，组成方程组，
解得：F1=1500N；F2=2000N；G动=100N．
把F1=1500N代入F1AB=G杆L2可得：1500N×4m=4000N×L2，
∴L2=1.5m．
答：（1）F1与F2的比值为3：4．
（2）动滑轮重G动为100N．
（3）金属杆的重心0距A端的距离为1.5m．
根据杠杆的平衡条件可知：F1AB=G杆L2，F2AC=G杆L2，
则F1AB=F2AC，
∴
| F1 |
| F2 |
| AC |
| AB |
| 3m |
| 4m |
| 3 |
| 4 |
（2）∵滑轮组的绳重、绳的伸长和轮轴问摩擦可以忽略，
∴η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额外 |
| F拉力h |
| F拉力h+G动h |
| F拉力 |
| F拉力+G动 |
即
| η1 |
| η2 |
| ||
|
| F1 |
| F1+G动 |
| F2+G动 |
| F2 |
| 63 |
| 64 |
化简得：64F1（F2+G动）=63F2（F1+G动），
即：F1F2+64F1G动=63F2G动②．
（3）从图可知，有四段绳子吊着物体，则绳子末端的拉力就等于竖直向上的拉力和动滑轮重力的
| 1 |
| 4 |
从图可知，人对地面的压力就等于人的重力减去绳子末端的拉力，
∴
| FN1 |
| FN2 |
| G人-F绳拉1 |
| G人-F绳拉2 |
700N-
| ||
700N-
|
| 12 |
| 7 |
化简得：12F2-7F1+5G动=14000N③，
则
| F1 |
| F2 |
| AC |
| AB |
| 3m |
| 4m |
| 3 |
| 4 |
解得：F1=1500N；F2=2000N；G动=100N．
把F1=1500N代入F1AB=G杆L2可得：1500N×4m=4000N×L2，
∴L2=1.5m．
答：（1）F1与F2的比值为3：4．
（2）动滑轮重G动为100N．
（3）金属杆的重心0距A端的距离为1.5m．
点评：本题考查了杠杆的平衡条件、机械效率的计算和拉力计算，关键是对公式公式变形的理解和应用，考查的知识点较多，这就需要学生对公式和公式变形有一定的理解，有一定的难度．
练习册系列答案
相关题目
（2010?朝阳区一模）图是表示甲、乙两种物质“质量与体积关系”的图象．由图可知，物质
（2010?朝阳区一模）小阳想利用两块电压表和阻值已知的电阻R0测量电阻Rx的阻值．他选择了满足实验要求的电源、电压表V1和V2，并连接了部分电路如图所示．，
（2010?朝阳区一模）小阳和小华有一段对话（见图）．请你利用身边的物品或实验器材设计一个实验，证明他们的观点是不正确的．
（2010?朝阳区一模）如图所示电路中，灯泡L标有“3V”且灯丝电阻不变．电源两端电压为U保持不变，R1为定值电阻，R2为滑动变阻器．当只闭合开关S、S1时，灯泡的功率是额定功率的四分之一．当只闭合开关S、S2时，调节滑动变阻器的滑片P，使其位于a点时（图中表示a点的大致位置），灯泡正常发光，电流表的示数是0.3A，滑动变阻器的功率为Pa；保持开关状态不变，滑动变阻器的滑片P移至b端时，滑动变阻器接入电路的电阻最大，此时灯泡的功率是额定功率的九分之一，滑动变阻器的功率为Pb，且知Pa：Pb=9：5．