Question

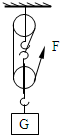用一个动滑轮、一个定滑轮组成的滑轮组来匀速提升重物G，如图所示，已知物重G=600N，拉力F=250N，求在重物升高0.5m的过程中，所做的有用功，额外功，及机械效率为多大？若所提升重物重力为750N，拉力为多大？此时的机械效率为多大？（不计绳重和摩擦力）．

Answer 1

分析：（1）由图可知，滑轮组绳子的有效股数为3，根据s=nh求出绳子自由端移动的距离，根据W=Gh求出有用功，根据W=Fs求出总功，额外功等于总功和有用功的差值，再根据效率公式求出滑轮组的机械效率；
（2）先根据F=

1

n

（G+G_动）求出动滑轮的重力，再根据F=

1

n

（G+G_动）求出提升重物重力为750N时的拉力，最后根据η=

W有

W总

=

Gh

Fs

=

Gh

Fnh

=

G

nF

求出此时滑轮组的机械效率．

解答：解：（1）由图可知，n=3，
绳子自由端移动的距离s=nh=3×0.5m=1.5m，
有用功W_有=Gh=600N×0.5m=300J，
总功W_总=Fs=250N×1.5m=375J，
额外功W_额=W_总-W_有=375J-300J=75J；
滑轮组的机械效率η=

W有

W总

=

300J

375J

=80%；
（2）根据F=

1

n

（G+G_动）可得：
G_动=nF-G=3×250N-600N=150N，
提升重物重力为750N时的拉力F′=

1

n

（G′+G_动）=

1

3

×（750N+150N）=300N，
由η=

W有

W总

=

Gh

Fs

=

Gh

Fnh

=

G

nF

可得：
此时滑轮组的机械效率η′=

G′

nF

=

750N

3×300N

≈83.3%．
答：在重物升高0.5m的过程中，所做的有用功为300J，额外功为75J，机械效率为80%；若所提升重物重力为750N，拉力为300N，此时的机械效率约为83.3%．

点评：本题考查了功和机械效率的计算，关键是明确有用功和总功、额外功之间的关系以及公式F=

1

n

（G+G_动）、η=

W有

W总

=

Gh

Fs

=

Gh

Fnh

=

G

nF

的灵活应用．