题目内容
某人自上午10点整从起点出发,途经三段不同的路程,首先是上坡路,然后是较平直的路,最后是一段下坡路,三段路的长度相同,在这三段路上行进的速度之比1:2:3,此人在下午2点整到达终点,则此人在正午12点时行到
- A.上坡路段
- B.平直路段
- C.下坡路段
- D.无法判断
A
分析:设上坡路上的速度为v,则平直、下坡路上的速度为2v、3v,知道三段路的长度相同,求出三段路程用的时间,根据用的总时间为4h,求出走上坡路上用的时间,从而判断12点行到哪里?
解答:设上坡路程、时间、速度分别为:s1、t1、v1,平路:s2、t2、v2,下坡路:s3、t3、v3,
由题意得:s1=s2=s3=s,t1+t2+t3=4h,v1:v2:v3=1:2:3.
设v1=v,则v2=2v,v3=3v.
t1=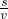 ,
,
t2=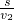 =
=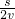 =
= t1,
t1,
t3=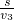 =
=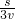 =
= t1,
t1,
t1+t2+t3=4h,
即:t1+ t1+
t1+ t1=4h,
t1=4h,
解得:t1=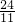 h≈2.18h,
h≈2.18h,
所以此人在正午12点(两小时)时行到上坡路.
故选A.
点评:本题考查了速度公式的应用,根据时间关系列方程求出每段路程用的时间是本题的关键.
分析:设上坡路上的速度为v,则平直、下坡路上的速度为2v、3v,知道三段路的长度相同,求出三段路程用的时间,根据用的总时间为4h,求出走上坡路上用的时间,从而判断12点行到哪里?
解答:设上坡路程、时间、速度分别为:s1、t1、v1,平路:s2、t2、v2,下坡路:s3、t3、v3,
由题意得:s1=s2=s3=s,t1+t2+t3=4h,v1:v2:v3=1:2:3.
设v1=v,则v2=2v,v3=3v.
t1=
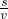 ,
,t2=
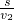 =
=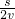 =
= t1,
t1,t3=
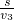 =
=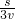 =
= t1,
t1,t1+t2+t3=4h,
即:t1+
 t1+
t1+ t1=4h,
t1=4h,解得:t1=
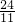 h≈2.18h,
h≈2.18h,所以此人在正午12点(两小时)时行到上坡路.
故选A.
点评:本题考查了速度公式的应用,根据时间关系列方程求出每段路程用的时间是本题的关键.

练习册系列答案
相关题目