��Ŀ����
����Ŀ��һ�����ŵ�Բ�����������������200cm2 �� װ��12cm���ˮ��������M�߳�Ϊ10cm����20N����ϸ�����ҷ���ˮ�У���![]() �����¶��ˮ�棬��ͼ��ʾ������
�����¶��ˮ�棬��ͼ��ʾ������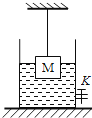
��1��������M���ܶ�
��2��
������M�ܵ��ĸ����Լ���ʱˮ�������ײ���ѹǿ
��3������ͼʾ״̬��ʼ��ͨ������K������ˮ����������ˮ���½���2cmʱ��ϸ���պñ����ϣ���ϸ���ܳ��ܵ���������Ƕ��٣���gȡ10N/Kg��ˮ���ܶ�Ϊ1.0��103Kg/m3����
���𰸡�
��1��
����𡿣�1��������M������mM=![]() =
=![]() =2kg��
=2kg��
���ΪVA=L3=��10cm��3=1000cm3=1��10��3m3��
���ԣ��ܶȦ�A=![]() =
=![]() =2��103kg/m3��
=2��103kg/m3��
��������M���ܶ�Ϊ2��103kg/m3.
��2��
�����������ϸ�����ҷ���ˮ�У���![]() �����¶��ˮ�棬��
�����¶��ˮ�棬��
V��1=��1��![]() ��
��![]() =
=![]() ��1��
��1��![]()
![]() =8��
=8��![]() m3��
m3��
�ܵ��ĸ���Ϊ��
F��1=��ˮgV��1=1.0��103kg/m3��10N/kg��8��10��4m3=8N��
��A����ˮ�к�ˮ��Ϊh��������Sh��=Sh+V��1��
��h��=h+![]() =0.12m+
=0.12m+![]() =0.16m��
=0.16m��
��ʱˮ�������ײ���ѹǿ��
p=��ˮgH��=1.0��103kg/m3��10N/kg��0.16m=1.6��103Pa��
��������M�ܵ��ĸ���Ϊ8N����ʱˮ�������ײ���ѹǿΪ1.6��103Pa.
��3��
�����ԭ��ʯ��M����ˮ�����Ϊh1=��1��![]() ��L=
��L=![]() ��10cm=8cm��
��10cm=8cm��
ˮ���½�2cmʱ������M����ˮ�����Ϊh2=h1��2cm=8cm��2cm=6cm��
��V��2=h2L2=6cm����10cm��2=600cm3=6��10��4m3��
F��2=��ˮgV��2=1.0��103kg/m3��10N/kg��6��10��4m3=6N��
�����Ӹձ�����ʱ�У�Fm+F��2=G��
����ϸ���ܳ��ܵ��������Fmax=G��F����=20N��6N=14N��
�𣺵�������ˮ���½���2cmʱ��ϸ���պñ����ϣ�ϸ���ܳ��ܵ����������14N��
����������1������������M�߳�Ϊ10cm�������������С�������ܶȹ�ʽ��=![]() ���ܶȣ�
���ܶȣ�
��2��������ϸ�����ҷ���ˮ�У���![]() �����¶��ˮ�棬���V�� �� ����F��=��ˮgV���������M�ܵ��ĸ�����
�����¶��ˮ�棬���V�� �� ����F��=��ˮgV���������M�ܵ��ĸ�����
��3�����������ĵ������ˮ���½�2cmʱ������M����ˮ�е����������F��=��ˮgV�����������ʱM�ܵ��ĸ����������������������������ϸ�����ܳ��ܵ����������
�����㾫����ͨ������������ĺϳ���Ӧ�ú�Һ���ѹǿ�ļ��㣬���������֪�������Ĵ�С�ͷ���������Ĵ�С�ͷ����Ϊ���ĺϳɣ��������ʱ��һ��Ҫע�����ķ��� ע�⣺ͬһֱ���ϵ���������������ͬʱ�������ش������е��κ�һ�����������෴������������С���ʱ������Ϊ0����С����ʱ������һ��С�ڽϴ���������ܴ��ڽ�С������Ҳ����С�ڽ�С������Һ���ڲ�ѹǿ�Ĺ�ʽ��p=��gh ��ָ�ܶ�,��λkg/m3,g=9.8N/kg, hָ���,��λ:m,ѹǿ��λ(Pa) ע�⣺h ָҺ�����ȣ���ij�㵽Һ��ľ��뼴���Խ����⣮