题目内容
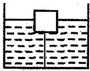 (2012?大庆)如图所示有一密度为0.6×103kg/m3、体积为10-3m3的正方体木块,用一条质量和体积可忽略不计的细绳,两端分别系于木块底部中心和柱形容器的中心.细绳能承受的最大拉力为3N(g取10N/kg).
(2012?大庆)如图所示有一密度为0.6×103kg/m3、体积为10-3m3的正方体木块,用一条质量和体积可忽略不计的细绳,两端分别系于木块底部中心和柱形容器的中心.细绳能承受的最大拉力为3N(g取10N/kg).(1)当细绳松弛,对木块没有拉力时,木块浸入水中的体积为
6×10-4
6×10-4
m3;(2)向容器内注水(水不溢出)直至细绳对木块的拉力达到最大值,在细绳处于断裂前一瞬间停止注水,此时木块浸入水中的体积为
9×10-4
9×10-4
m3.分析:(1)根据漂浮时浮力等于重力,可求出木块的排水体积,用到浮力公式与重力的公式;
(2)对此时的木块进行受力分析可知,此时浮力等于木块的重力加3N的拉力,据此可利用公式计算木块的排水体积.
(2)对此时的木块进行受力分析可知,此时浮力等于木块的重力加3N的拉力,据此可利用公式计算木块的排水体积.
解答:解:(1)木块漂浮且绳没有拉力时,
F浮=G木
即ρ水gv排=ρ木gv木
∴v排=
=
=6×10-4m3;
(2)绳子拉力最大时,木块受力平衡,则F浮′=ρ水gv排′=G木+F拉力,
v排′=
=
=9×10-4m3;
故答案为:(1)6×10-4;(2)9×10-4.
F浮=G木
即ρ水gv排=ρ木gv木
∴v排=
| ρ木v木 |
| ρ水 |
| 0.6×103kg/m3×10-3m3 |
| 1×103kg/m3 |
(2)绳子拉力最大时,木块受力平衡,则F浮′=ρ水gv排′=G木+F拉力,
v排′=
| ρ木gv木+F拉力 |
| ρ水g |
| 0.6×103kg/m3×10N/kg×10-3m3+3N |
| 1.0×103kg/m3×10N/kg |
故答案为:(1)6×10-4;(2)9×10-4.
点评:本题考查了阿基米德原理和平衡力的应用,重点是分析出木块在不同情况下受力情况,然后根据物体处于平衡状态受到平衡力即可求出所求的物理量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
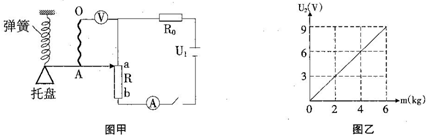
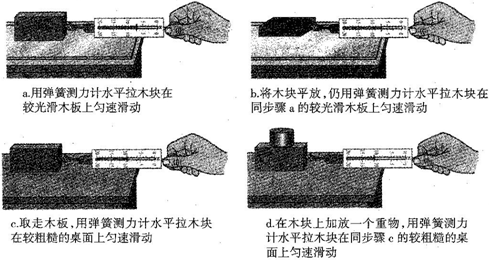
 (2012?大庆)如图所示的汽车总质量为1150kg,以72km/h的速度匀速行驶10km,若汽车所受阻力为汽车重力的0.1倍,每个轮胎与路面的接触面积为0.05m2.(g=10N/kg)
(2012?大庆)如图所示的汽车总质量为1150kg,以72km/h的速度匀速行驶10km,若汽车所受阻力为汽车重力的0.1倍,每个轮胎与路面的接触面积为0.05m2.(g=10N/kg)