题目内容
【题目】在如图所示的路中,电源电压保持不变,电阻R1的阻值为20欧,闭合电键S,两电流表的示数分别为0.8安和0.3安. 
①求电源电压U.
②求通过电阻R2的电流I2 .
③现用电阻R0替换电阻R1、R2中的一个,替换前后,只有一个电流表的示数发生了变化,且电源的电功率变化了0.6瓦,求电阻R0的阻值.
【答案】解:由电路图可知,R1与R2并联,电流表A测干路电流,电流表A1测电阻R1支路的电流. ①闭合电键S,两电流表的示数分别为0.8A和0.3A,
因并联电路中干路电流等于各支路电流之和,
所以,干路电流I=0.8A,通过电阻R1的电流I1=0.3A,
并联电路中各支路两端的电压相等,
所以,由欧姆定律可得,电源电压:
U=U1=I1R1=0.3A×20Ω=6V;
②由并联电路的电流特点可得,通过R2的电流:
I2=I﹣I1=0.8A﹣0.3A=0.5A;
③由题知,用电阻R0替换电阻R1、R2中的一个,替换前后,只有一个电流表的示数发生了变化;
若用R0替换电阻R1 , 则电流表A1所在支路的电阻发生变化,电流表A1的示数会发生变化,同时干路电流也会发生变化,即电流表A的示数发生变化,不符合题意;因此只能是用R0替换电阻R2;
替换前电源的电功率:
P总=UI=6V×0.8A=4.8W;
替换后电源的电功率变化了0.6W,则此时电源的电功率可能为:
P总′=P总+△P=4.8W+0.6W=5.4W,P总″=P总﹣△P=4.8W﹣0.6W=4.2W;
并联电路中各支路独立工作、互不影响,所以,替换前后R1的电流和功率均不变,
则R1消耗的功率:P1=UI1=6V×0.3A=1.8W;
因替换后R1与R0并联,且电源的电功率等于各电阻消耗功率之和,
所以,电阻R0消耗的功率可能为:
P0=P总′﹣P1=5.4W﹣1.8W=3.6W,P0′=P总″﹣P1=4.2W﹣1.8W=2.4W,
由P= ![]() 可得,R0的阻值可能为:
可得,R0的阻值可能为:
R0= ![]() =
= ![]() =10Ω,R0′=
=10Ω,R0′= ![]() =
= ![]() =15Ω,
=15Ω,
即电阻R0的阻值为10Ω或15Ω才能满足题中的要求.
答:①电源电压U为6V;
②通过电阻R2的电流I2为0.5A;
③现用电阻R0替换电阻R1、R2中的一个,替换前后,只有一个电流表的示数发生了变化,且电源的电功率变化了0.6瓦,电阻R0的阻值为10Ω或15Ω.
【解析】由电路图可知,R1与R2并联,电流表A测干路电流,电流表A1测电阻R1支路的电流.(1)根据并联电路的电压特点和欧姆定律求出电源的电压;(2)根据并联电路的电流特点求出通过R2的电流;(3)由题知,电阻R0替换电阻R1、R2中的一个,替换前后,只有一个电流表的示数发生了变化;根据并联电路的特点确定电阻R0所替换的电阻;根据题中条件利用P=UI求出替换前电源的电功率;再根据题意求出替换后电源的电功率;由并联电路的特点可知另一支路的电阻消耗的功率不变,且根据P=UI可求出该电阻消耗的功率;因电源的电功率等于各电阻消耗功率之和,据此可求出R0消耗的功率;最后利用P= ![]() 可得R0的阻值.
可得R0的阻值.
【考点精析】掌握欧姆定律及其应用是解答本题的根本,需要知道欧姆定律的应用: ① 同一个电阻,阻值不变,与电流和电压无关 但加在这个电阻两端的电压增大时,通过的电流也增大.(R=U/I) ② 当电压不变时,电阻越大,则通过的电流就越小.(I=U/R) ③ 当电流一定时,电阻越大,则电阻两端的电压就越大.(U=IR).

 阅读快车系列答案
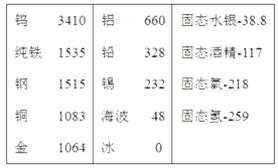
阅读快车系列答案【题目】小明用六个重力G均为10牛,体积不同的球体,研究放入球体前后容器底部受到水的压力增加量△F的情况.他分别将球体放入盛有等质量水的相同容器中,待球体静止,得到容器底部受到水的压力增加量△F,实验数据和实验现象如表
实验序号 | 1 | 2 | 3 | 4 | 5 | 6 |
放入的球体 | A | B | C | D | E | F |
△F(牛) | 5 | 6 | 8 | 10 | 10 | 10 |
实验现象 |
| |||||
(1)观察序号1或2或3中的实验现象并比较△F和G的大小关系,可得出的初步结论是:当放入的球体在水中沉底时, . 观察序号4或5或6中实验现象并比较△F和G的大小关系,可得出的初步结论是, .
(2)小明得出“在盛有等质量水的相同容器中,当放入球体的重力相同时,球体的体积越大,△F越大”的结论.由表中实验序号的现象,数据及相关条件可判断小明得出的结论不正确.
(3)分析表中序号1﹣6的现象,数据及相关条件,可得出:在盛有等质量水的相同容器中,当放入球体的重力相同时,体积越大,△F越大.