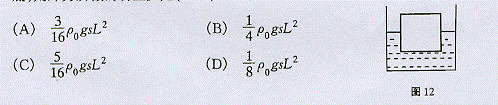题目内容
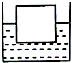 如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为
如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为| 1 |
| 2 |
分析:物体漂浮时,浮力等于物体的重力;根据浮力公式求出物体浸入水中的深度;物体处于平衡状态,对物体进行受力分析,求出F的大小,由于物体缓慢运动,所以可以认为是匀速运动,再求出物体在水中移动的距离,根据公式W=FS可求外力做的功.
思路:根据能量守恒,外力做功=水增加重力势能-物块减小重力势能,重点是水的重心变化的位置;质量就是排开水的质量.
思路:根据能量守恒,外力做功=水增加重力势能-物块减小重力势能,重点是水的重心变化的位置;质量就是排开水的质量.
解答:解:物块重心降低
L,物块重力做功W1=
ρ0gSL
L=
ρ0gSL2;
设用外力将物块按入水底后,杯内水的高度为L′,
则2SL′=2SL+S
L,解得L′=
L,
在末状态,水面高出物块上表面
L,这相当于原来初状态图示中物块下面的那部分水全部升至末态的物块之上,这部分水(ρ0×0.5LS)升高了(1.125-0.25)L=0.875L,
其重力势能增加△W=ρ0×0.5LSg×0.875L,减去物块减小的重力势能W1=
ρ0×SL×
,
即为外力至少做的功W=△W-W1=ρ0×0.5LSg×0.875L-
ρ0×SL×
=
ρ0gSL2
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
设用外力将物块按入水底后,杯内水的高度为L′,
则2SL′=2SL+S
| 1 |
| 2 |
| 5 |
| 4 |
在末状态,水面高出物块上表面
| 1 |
| 4 |
其重力势能增加△W=ρ0×0.5LSg×0.875L,减去物块减小的重力势能W1=
| 1 |
| 2 |
| L |
| 2 |
即为外力至少做的功W=△W-W1=ρ0×0.5LSg×0.875L-
| 1 |
| 2 |
| L |
| 2 |
| 3 |
| 16 |
故选A.
点评:本题考查压力、浮力、做功等的计算,对于这类综合题目,要分成几个小步骤逐个分析,结合对应的物理公式求解.

练习册系列答案
相关题目
 的速度向右运动,在A处环被挡住而立即停止,A离右墙的水平距离也为L。不计空气阻力,已知当地的重力加速度为g。试求:
的速度向右运动,在A处环被挡住而立即停止,A离右墙的水平距离也为L。不计空气阻力,已知当地的重力加速度为g。试求:
 如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为
如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为 ρ0,现用外力将物块按入水底,则外力所做的功至少是
ρ0,现用外力将物块按入水底,则外力所做的功至少是 ρ0gsL2
ρ0gsL2 ρ0gsL2
ρ0gsL2 ρ0gsL2
ρ0gsL2 ρ0gsL2
ρ0gsL2 ρ,现用外力将物块按入水底,则外力所做的功至少是( )
ρ,现用外力将物块按入水底,则外力所做的功至少是( )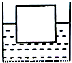
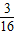 ρgsL2
ρgsL2 ρgsL2
ρgsL2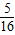 ρgsL2
ρgsL2 ρgsL2
ρgsL2