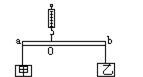
题目内容
如图所示,AB为一轻质杠杆,C为边长10cm的正方体铜块浸在水中,OA:OB=3:1,整个装置处于平衡状态,求物体D的重力.(铜的密度为8.9g/cm3,绳重、滑轮重、摩擦均不计,g=10N/kg)


分析:已知正方体的边长,可以求出它的体积,根据密度公式求出铜块的质量,进一步求出其重力;再利用浮力公式求出浮力的大小,由滑轮组拉力公式可以求出绳子对A点向下的拉力,然后由杠杆平衡条件可以求出D的重力的大小.
解答:解:C为边长10cm的正方体铜块,正方体铜块的体积V=10-3m3;
∵ρ=
,
∴质量m=ρV=8.9×103kg/m3×10-3m3=8.9kg;
重力G=mg=8.9kg×10N/kg=89N;
受到的浮力:
F浮=ρ水gV=1×103kg/m3×10N/kg×10-3m3=10N;
所以A点受到的向下的拉力:
F=
=
=39.5N;
OA为力F的力臂;OB为物体D的力臂,
根据杠杆的平衡条件F×OA=GD×OB;可知,GD=
=
=118.5N.
答:物体D的重力为118.5N.
∵ρ=
| m |
| V |
∴质量m=ρV=8.9×103kg/m3×10-3m3=8.9kg;
重力G=mg=8.9kg×10N/kg=89N;
受到的浮力:
F浮=ρ水gV=1×103kg/m3×10N/kg×10-3m3=10N;
所以A点受到的向下的拉力:
F=
| G-F浮 |
| 2 |
| 89N-10N |
| 2 |
OA为力F的力臂;OB为物体D的力臂,
根据杠杆的平衡条件F×OA=GD×OB;可知,GD=
| F×OA |
| OB |
| 39.5N×3 |
| 1 |
答:物体D的重力为118.5N.
点评:本题考查了物体质量、拉力大小的计算,熟练应用密度公式的变形公式、滑轮组拉力公式、杠杆平衡条件,即可正确解题.

练习册系列答案
相关题目
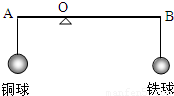
 如图所示,AB为一轻质杠杆,O为支点,在O点两侧分别悬挂体积相等的实心铜球和实心铁球,杠杆在水平位置平衡.若将两球分别远离O点向外移动相同的距离(未脱离杠杆),则( )
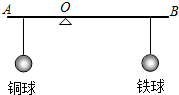
如图所示,AB为一轻质杠杆,O为支点,在O点两侧分别悬挂体积相等的实心铜球和实心铁球,杠杆在水平位置平衡.若将两球分别远离O点向外移动相同的距离(未脱离杠杆),则( ) 如图所示,AB为一轻质杠杆,O为支点,BO=2AO,AB两端分别悬挂实心铜球和实心铁球,杠杆在水平位置平衡,若将两球同时浸没在某液体中,液体的密度小于铜和铁的密度,则( )
如图所示,AB为一轻质杠杆,O为支点,BO=2AO,AB两端分别悬挂实心铜球和实心铁球,杠杆在水平位置平衡,若将两球同时浸没在某液体中,液体的密度小于铜和铁的密度,则( )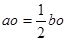 ,弹簧秤的读数为6牛,则甲的重力为____牛。
,弹簧秤的读数为6牛,则甲的重力为____牛。