Question

（2012?津南区二模）如图（甲）所示是使用吊车打捞浸没水下重物的示意图．水下有一个圆柱形重物，在整个打捞过程中，吊车以υ m/s速度竖直向上提拉重物．图（乙）是此过程中吊车拉动重物的功率P随时间t的变化图象，设t=0时开始提升重物，忽略机械的重力、各部件间的摩擦和水的阻力，g取10N/㎏，求：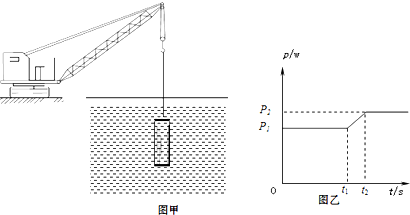
（1）圆柱型重物沉在水底时，上表面受到水的压强是多大？
（2）圆柱型重物的密度？

Answer 1

分析：（1）根据图象，搞清上表面所处的深度h，并运用液体压强公式p=ρgh，可求出上表面受到的压强．
（2）充分利用图象中功率与拉力的关系P=Fv，准确分析物体的受力情况，可求出重物的密度．

解答：解：（1）从图象可知，当重物未露出水面时吊车拉动重物的功率P为P₁，所用的时间为t₁；
重物上表面距离水面的距离为h₁=vt₁；上表面受到水的压强为：p=ρgh₁=ρgvt₁．
（2）当重物未露出水面时，重物受到三个力的作用，即拉力F₁、重力G、浮力F_浮；
三个力的关系为F₁=G-F_浮；且有P₁=F₁v．
当重物全部露出水面时，重物受到两个力的作用，即拉力F₂、重力G；
两个力的关系为F₂=G；且有P₂=F₂v．
由F₂=G和P₂=F₂v得：G=

P2

v

．
由P₁=F₁v得：F₁=

P1

v

；
将F₁=

P1

v

和G=

P2

v

代入F₁=G-F_浮中可得：F_浮=

P2

v

-

P1

v

=

P2-P1

v

；
再由阿基米德原理知F_浮=ρgV_排，则V_物=V_排=

F浮

ρg

=

P2-P1 v

ρg

=

P2-P1

ρgv

．
则重物的密度为ρ_物=

m

V物

=

G g

P2-P1 ρgv

=

ρGv

P2-P1

．
答：（1）圆柱型重物沉在水底时，上表面受到水的压强是ρgvt₁．
（2）圆柱型重物的密度为

ρGv

P2-P1

．

点评：此题是一道很难的力学综合题，熟练运用液体压强公式、阿基米德原理以及功率的公式；准确分析图象中的信息，方可解答此题．