题目内容
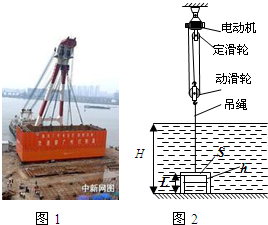（2013?东城区一模）我国是世界上第一个成功完成海底沉船整体打捞的国家，如图1是“南海1号”沉船打捞出水的情况．所谓整体打捞，就是将沉船与其周围泥沙按原状固定在特殊的钢制沉箱内一次性吊浮起运，沉箱是一种用金属制成，形状像箱子，下面没有底，可以罩住整个沉船的设备．沉箱四周安放了气囊，起吊过程气体膨胀，产生巨大的浮力，起到助浮的作用．如图2所示是与上述原理相似的简化装置：一个质量为11.7t的钢制沉箱倒扣在深度H=20m的水底，箱内腔体的横截面积S=10m2、高为L=4m，可忽略重力和体积的充气装置使箱内封入高h为0.5m的空气．现用吊绳将沉箱打捞至水面，吊绳与滑轮组及电动机相连可控制沉箱匀速上升，ρ钢=7.8×103kg/m3，ρ海水取1×103kg/m3，g=10N/kg，水的阻力、摩擦和绳重不计．问：（1）沉箱倒扣在海底时，沉箱的上表面所受海水的压强是多大？（此问不计沉箱上表面的厚度）
（2）若使沉箱能够从海底被吊起，吊绳的拉力至少多大？
（3）沉箱上升至到达水面之前的过程中，因压强减小箱内空气体积增大，已知h为0.5m时，滑轮组的机械效率η1=98%，那么当h为1m时，滑轮组的机械效率η2是多少？（结果保留整数）
（4）假设腔内空气的高度h一直未达到腔体的高度L，通过计算说明从起吊到沉箱上表面到达海面的过程中，电动机是否必须一直做功？
分析：（1）已知水的深度和沉箱的高度，可以得到沉箱上表面所在水的深度，已知水的密度和深度，利用公式p=ρgh计算沉箱上表面所受海水的压强；
（2）沉箱被拉起的过程中，受到三个力的作用：重力、拉力和浮力．已知沉箱的质量，可以得到重力；要得到沉箱受到的浮力，需要知道沉箱排开海水的体积；
（3）沉箱上升过程中，应用水的压强的减小，所以箱内空气体积增大，沉箱排开水的体积增大，受到的浮力增大，已知沉箱重力和此时的浮力，可以得到此时的拉力；在前后两次提升过程中，做的额外功都是克服动滑轮重做的功，根据机械效率的公式得到第二次的效率；
（4）沉箱在上升过程中，排开海水的体积一直增大，受到的浮力相应增大，当等于重力时，拉力为零；当浮力大于重力时，不需要拉力．
（2）沉箱被拉起的过程中，受到三个力的作用：重力、拉力和浮力．已知沉箱的质量，可以得到重力；要得到沉箱受到的浮力，需要知道沉箱排开海水的体积；
（3）沉箱上升过程中，应用水的压强的减小，所以箱内空气体积增大，沉箱排开水的体积增大，受到的浮力增大，已知沉箱重力和此时的浮力，可以得到此时的拉力；在前后两次提升过程中，做的额外功都是克服动滑轮重做的功，根据机械效率的公式得到第二次的效率；
（4）沉箱在上升过程中，排开海水的体积一直增大，受到的浮力相应增大，当等于重力时，拉力为零；当浮力大于重力时，不需要拉力．
解答：已知：ρ海水=1×103kg/m3 H=20m L=4m g=10N/kg m=11.7t=1.17×104kg ρ钢=7.8×103kg/m3 S=10m2 h1=0.5m η1=98% h2=1m
求：（1）p=？（2）F最小=？（3）η2=？（4）h3=？
解：（1）沉箱倒扣在海底时，沉箱的上表面所受海水的压强为p=ρ海水gh=1×103kg/m3×10N/kg×（20m-4m）=1.6×105Pa；
（2）∵ρ=
∴沉箱在水底时，腔体壁与底占有的体积V0=
=
=1.5m3
空气占有的体积V=S?h1=10m2×0.5m=5m3
∴沉箱受到的浮力F浮1=ρ水g（V0+V）=1×103kg/m3×10N/kg×（1.5m3+5m3）=6.5×104N
所以拉动沉箱的最小的力F最小=mg-F浮1=1.17×104kg×10N/kg-6.5×104N=5.2×104N；
（3）当h1=0.5m时，η1=98%，对应吊绳上的拉力F最小=5.2×104N
当h2=1m时，对应此时空气的体积V2=S?h2=10m2×1m=10m3
此时沉箱受到的浮力为F浮2=ρ水g（V0+V2）=1×103kg/m3×10N/kg×（1.5m3+10m3）=11.5×104N
吊绳上的拉力是F较小=mg-F浮2=1.17×104kg×10N/kg-11.5×104N=2×103N；
由η=
=
得：η1=
，η2=
，
将上述数据代入，解得：η2=65%
（4）如果在到达水面前，h增加到h3时，沉箱所受浮力等于沉箱的重力，
即1×103kg/m3×10N/kg×（1.5m3+10m2×h3）=1.17×104kg×10N/kg
解得h3=1.02m
之后浮力仍将进一步增大，所以电动机不一定需要一直做功．
答：（1）沉箱倒扣在海底时，沉箱的上表面所受海水的压强是1.6×105Pa；
（2）若使沉箱能够从海底被吊起，吊绳的拉力至少为5.2×104N；
（3）当h为1m时，滑轮组的机械效率η2是65%；
（4）如果在到达水面前，h增加到1.02m时，沉箱所受浮力等于沉箱的重力，之后浮力仍将进一步增大，所以电动机不一定需要一直做功．
求：（1）p=？（2）F最小=？（3）η2=？（4）h3=？
解：（1）沉箱倒扣在海底时，沉箱的上表面所受海水的压强为p=ρ海水gh=1×103kg/m3×10N/kg×（20m-4m）=1.6×105Pa；
（2）∵ρ=
| m |
| V |
∴沉箱在水底时，腔体壁与底占有的体积V0=
| m |
| ρ钢 |
| 1.17×104kg |
| 7.8×103kg/m3 |
空气占有的体积V=S?h1=10m2×0.5m=5m3
∴沉箱受到的浮力F浮1=ρ水g（V0+V）=1×103kg/m3×10N/kg×（1.5m3+5m3）=6.5×104N
所以拉动沉箱的最小的力F最小=mg-F浮1=1.17×104kg×10N/kg-6.5×104N=5.2×104N；
（3）当h1=0.5m时，η1=98%，对应吊绳上的拉力F最小=5.2×104N
当h2=1m时，对应此时空气的体积V2=S?h2=10m2×1m=10m3
此时沉箱受到的浮力为F浮2=ρ水g（V0+V2）=1×103kg/m3×10N/kg×（1.5m3+10m3）=11.5×104N
吊绳上的拉力是F较小=mg-F浮2=1.17×104kg×10N/kg-11.5×104N=2×103N；
由η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额 |
| F最小 |
| F最小+G0 |
| F较小 |
| F较小+G0 |
将上述数据代入，解得：η2=65%
（4）如果在到达水面前，h增加到h3时，沉箱所受浮力等于沉箱的重力，
即1×103kg/m3×10N/kg×（1.5m3+10m2×h3）=1.17×104kg×10N/kg
解得h3=1.02m
之后浮力仍将进一步增大，所以电动机不一定需要一直做功．
答：（1）沉箱倒扣在海底时，沉箱的上表面所受海水的压强是1.6×105Pa；
（2）若使沉箱能够从海底被吊起，吊绳的拉力至少为5.2×104N；
（3）当h为1m时，滑轮组的机械效率η2是65%；
（4）如果在到达水面前，h增加到1.02m时，沉箱所受浮力等于沉箱的重力，之后浮力仍将进一步增大，所以电动机不一定需要一直做功．
点评：此题以海上打捞沉箱为素材，设计了一道包含机械效率、滑轮组的特点、阿基米德原理的应用及重力与质量的关系、液体压强的计算等内容的综合性很强的力学题，覆盖面广，难度大，解决的前提是掌握扎实的基础知识，能够迅速的提取有价值信息．
练习册系列答案
阅读快车系列答案
相关题目
（2013?东城区一模）在如图所示的装置内，分别用两个试管给10g水和10g油加热，其温度随时间变化的关系图象如图所示，水的比热容是4.2×103J/（kg?℃），则（ ）
（2013?东城区一模）在如图所示电路中，电源电压保持不变，闭合开关S，电压表V1的示数用U1表示，电压表V2的示数用U2表示，电流表A的示数用I表示，定值电阻和滑动变阻器的阻值分别用R1、R2表示．当滑动变阻器的滑片P向右移动时，下列说法一定正确的是（ ）