题目内容
将一木块放在水中,它露出水面部分的体积V1是24cm3,将露出水面部分完全截去后再放入水中,它露出水面部分的体积V2是16cm3,求木块的密度和原来的体积各为多少?
分析:假设木块的体积为v,排开水的体积为V-32cm3,利用阿基米德原理F浮=ρ水V排g和漂浮条件F浮=G=mg=ρ木Vg得出一个关于V、ρ木的方程;
把露出水面的部分截去后,剩余木块的体积为上面排开水的体积,再利用同样的道理得出一个关于V、ρ木的方程;
联立方程组求解.
把露出水面的部分截去后,剩余木块的体积为上面排开水的体积,再利用同样的道理得出一个关于V、ρ木的方程;
联立方程组求解.
解答:解:假设木块的体积为V,排开水的体积为V-24cm3,
∵木块漂浮,
∴F浮=G=mg=ρ木Vg,
又∵F浮=ρ水V排g,
∴ρ水V排g=ρ木Vg,
ρ水(V-24cm3)g=ρ木Vg;---------------①
把露出水面的部分截去后,剩余木块的体积为上面排开水的体积,排开水的体积为V-24cm3-16cm3,
∵木块漂浮,
∴F浮′=G′=m′g=ρ木V′g,
又∵F浮′=ρ水V排′g,
∴ρ水V排′g=ρ木V′g,
即:ρ水(V-24cm3-16cm3)g=ρ木(V-24cm3)g;--------------②
由①②联立解得:
V=72cm3,ρ木=0.66×103kg/m3.
答:木块的密度是0.66×103kg/m3.原来的体积为72cm3.
∵木块漂浮,
∴F浮=G=mg=ρ木Vg,
又∵F浮=ρ水V排g,
∴ρ水V排g=ρ木Vg,
ρ水(V-24cm3)g=ρ木Vg;---------------①
把露出水面的部分截去后,剩余木块的体积为上面排开水的体积,排开水的体积为V-24cm3-16cm3,
∵木块漂浮,
∴F浮′=G′=m′g=ρ木V′g,
又∵F浮′=ρ水V排′g,
∴ρ水V排′g=ρ木V′g,
即:ρ水(V-24cm3-16cm3)g=ρ木(V-24cm3)g;--------------②
由①②联立解得:
V=72cm3,ρ木=0.66×103kg/m3.
答:木块的密度是0.66×103kg/m3.原来的体积为72cm3.
点评:本题关键:一是阿基米德原理和漂浮条件的灵活运用,二是利用好两种情况下:V=V排+V露.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
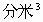 的圆柱形容器内注入3升水,已知它的底面积为250
的圆柱形容器内注入3升水,已知它的底面积为250 .现在将一木块放在水中,木块静止时有2/3的体积浸在水中.若再将一个质量为500克的铁块放在木块上,木块刚好全部浸没在水中.此时水是否会溢出?容器底部受到的压强比放入木块及铁块前增大多少?
.现在将一木块放在水中,木块静止时有2/3的体积浸在水中.若再将一个质量为500克的铁块放在木块上,木块刚好全部浸没在水中.此时水是否会溢出?容器底部受到的压强比放入木块及铁块前增大多少?