题目内容
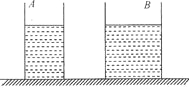
【题目】如图所示,两个盛有等高液体的圆柱形容器 A 和 B ,底面积不同( S A < S B ),液体对容器底部的压强相等.现将甲球浸没在 A 容器的液体中,乙球浸没在 B 容器的液体中,容器中均无液体溢出,若此时液体对各自容器底部的压力相等,则一定是( )
A. 甲球的质量小于乙球的质量
B. 甲球的质量大于乙球的质量
C. 甲球的体积小于乙球的体积
D. 甲球的体积大于乙球的体积
【答案】D
【解析】开始时,液体对容器底部的压强相等;即PA=PB,深度h相同,根据液体的压强公式P=ρgh可得容器内的液体密度ρ相同;又SA<SB,PA=PB,根据压强的定义式P![]() ,变形后得F=PS;故有FA<FB;后来,浸没甲、乙球后,液体对各自容器底部的压力相等,即FA=FB;可见B容器内增大的液体压力小于A容器内增大的液体压力,即△FB<△FA;根据F=PS得:△pBSB<△pASA;再根据p=ρgh得:ρg△hBSB<ρg△hASA;即△hBSB<△hASA;即△VB<△VA;又因为增大的体积△V就等于球的体积,即△V=V球;故有V乙<V甲;故D正确;C错误;由于两球的空心、实心情况不知,且两球的密度大小不知;故两球的质量大小关系不定;故AB错误;故选D.
,变形后得F=PS;故有FA<FB;后来,浸没甲、乙球后,液体对各自容器底部的压力相等,即FA=FB;可见B容器内增大的液体压力小于A容器内增大的液体压力,即△FB<△FA;根据F=PS得:△pBSB<△pASA;再根据p=ρgh得:ρg△hBSB<ρg△hASA;即△hBSB<△hASA;即△VB<△VA;又因为增大的体积△V就等于球的体积,即△V=V球;故有V乙<V甲;故D正确;C错误;由于两球的空心、实心情况不知,且两球的密度大小不知;故两球的质量大小关系不定;故AB错误;故选D.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】某同学在“探究影响电阻大小的因素”时,从实验室中选出符合要求的学生电源、滑动变阻器、电流表、开关、导线若干以及四根不同的合金丝,组成图所示电路,合金丝的参数如下表所示。下列说法正确的是( )
合金丝 | 材料 | 长度/m | 横截面积/mm2 |
a | 镍铬合金丝 | 1.0 | 0.3 |
b | 镍铬合金丝 | 1.0 | 0.1 |
c | 镍铬合金丝 | 0.5 | 0.1 |
d | 锰铜合金丝 | 0.5 | 0.1 |
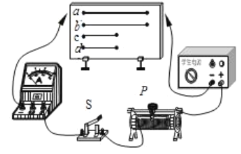
A.选用a、b两根合金丝,可探究合金丝的电阻与其横截面积是否有关
B.选用a、c两根合金丝,可探究合金丝的电阻与其长度是否有关
C.选用b、c两根合金丝,可探究合金丝的电阻与其长度是否有关
D.选用a、d两根合金丝,可探究合金丝的电阻与其材料是否有关