题目内容
（2010?密云县一模）如图所示，杠杆AOB及支架是一个固连在一起的整体，AO：BO=5：2．图中正方体D与水平地面的接触面积为8×10-2m2，物体B的质量为2kg．当物体A的质量为9.2kg时，杠杆在水平位置上平衡，物体D对水平地面的压强为4000pa．当把物体A换为质量为39.5kg的物体C，支点向左移，使AO：BO=4：3时，杠杆仍在水平位置上平衡，物体D对水平地面的压力为零．（杠杆、支架和托盘的重力不计，g取10N/kg．拉物体B的细绳系于物体B上表面中央并沿竖直方向）求：（1）动滑轮的质量．
（2）物体D的质量．
分析：对物体正确受力分析，应用平衡条件及杠杆平衡条件列方程，然后可以求出动滑轮与物体D的质量．
解答：解：当物体A质量为9.2kg时，动滑轮、物体A、杠杆及物体D受力如图1所示，
当把物体A换为质量为39.5kgC时，动滑轮、物体C、杠杆及物体D受力如图2所示，
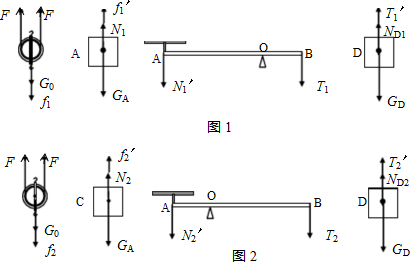
其中f′=f1，N1′=N1，T1′=T1，
GB=mBg=20N，GA=mAg=92N，GC=mCg=395N，
由题干图示可知F=GB=20N，
ND1=pS=4000Pa×8×10-2m2=320N，
由平衡条件得：
2F=G0+f1，即40N=G0+f1 ①，
f1+N1=GA，即f1+N1=92N ②，
T1+ND1=GD，即T1+320N=GD ③，
由杠杆平衡条件得：N1×AO=T1×0B ④，
由①②解得：N1=G0+52N ⑤，（G0+52N）×AO=（GD-320N）×OB ⑥，
2F=G0+f2，即：40N=G0+f2 ⑦，
f2+N2=GC，即f2+N2=395N ⑧，T2=GD⑨，
由⑦⑧解得：N2=G0+345N ⑩，
（G0+3450N）×AO=GD×OB （11）
将AO：B0=2：5代入⑥⑩解得：GD=500N，G0=20N，
∵G=mg，∴所以动滑轮的质量m0=
=
=2kg，
D的质量mD=
=
=50kg．
答：（1）动滑轮的质量为2kg．
（2）物体D的质量为50kg．
当把物体A换为质量为39.5kgC时，动滑轮、物体C、杠杆及物体D受力如图2所示，
其中f′=f1，N1′=N1，T1′=T1，
GB=mBg=20N，GA=mAg=92N，GC=mCg=395N，
由题干图示可知F=GB=20N，
ND1=pS=4000Pa×8×10-2m2=320N，
由平衡条件得：
2F=G0+f1，即40N=G0+f1 ①，
f1+N1=GA，即f1+N1=92N ②，
T1+ND1=GD，即T1+320N=GD ③，
由杠杆平衡条件得：N1×AO=T1×0B ④，
由①②解得：N1=G0+52N ⑤，（G0+52N）×AO=（GD-320N）×OB ⑥，
2F=G0+f2，即：40N=G0+f2 ⑦，
f2+N2=GC，即f2+N2=395N ⑧，T2=GD⑨，
由⑦⑧解得：N2=G0+345N ⑩，
（G0+3450N）×AO=GD×OB （11）
将AO：B0=2：5代入⑥⑩解得：GD=500N，G0=20N，
∵G=mg，∴所以动滑轮的质量m0=
| G0 |
| g |
| 20N |
| 10N/kg |
D的质量mD=
| GD |
| g |
| 500N |
| 10N/kg |
答：（1）动滑轮的质量为2kg．
（2）物体D的质量为50kg．
点评：本题难度较大，对物体正确受力分析是正确解题的前提与关键，应用平衡条件、杠杆平衡条件即可正确解题．
练习册系列答案
相关题目
（2010?密云县一模）小英同学用实验探究某种液体的质量和体积的关系，她根据测量的数据描绘了该液体的质量和体积关系的图象，如图所示．请你根据图象回答下列问题．