Question

（2012?西城区一模）某建筑工地上，甲、乙两位工人采用如图35所示的装置提升一个重为G₁的货箱．当两人同时对绳索施加竖直向下的等大的拉力，使货箱以速度υ平稳上升时，甲、乙两人对地面的压力之比为3：4．之后两位工人用此装置提升另一个重为G₂的货箱，使货箱仍以速度υ平稳上升．用此装置先、后两次提升不同的货箱，两位工人拉力总共做的功随时间变化的图象如图36中①、②所示．已知工人甲重650N，工人乙重700N；G₁：G₂=3：1，此装置中两个滑轮组的规格完全相同．不计绳重和轴摩擦．求：
（1）第一个货箱的重力；
（2）提升第二个货箱整个装置的机械效率．

Answer 1

分析：（1）两工人拉起货箱时，对货箱和动滑轮进行受力分析，可得关系式8F₁=2G_动+G₁，对工人甲、乙受力分析可得
关系式N_甲+F₁=G_甲和N_乙+F₁=G_乙，进而求出压力之比 

N甲

N乙

，从而求出拉力F₁；
当货箱1和2上升时，W=Pt，在相同的时间t内，由题中W-t图象可知，

W总1

W总2

=

P总1t

P总2t

=

4000J

1600J

=

5

2

，而P=Fv，速度v相同，可得 关系式2G₁=5G₂+6G_动，以上几个关系式联立可解得G₁、G₂、G_轮的大小；
（2）根据η=

W有用2

W总2

=

G2h

G2h+ 2G轮h

 求提升第二个货箱整个装置的机械效率．

解答：解：
（1）两工人拉起货箱时，货箱和动滑轮受力如右图所示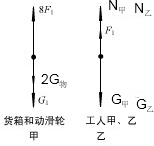，则
8F₁=2G_动+G₁-----①
工人甲、乙受力如右图所示，则：
N_甲+F₁=G_甲，--------②
N_乙+F₁=G_乙，---------③
 

N甲

N乙

=

G甲-F1

G乙-F1

=

3

4

，------④
解得：
F₁=4G_甲-3G_乙=4×650N-3×700N=500N；
货箱1和2上升时，W=Pt，在相同的时间t内，由题中W-t图象可知：

W总1

W总2

=

P总1t

P总2t

=

4000J

1600J

=

5

2

，则：

P总1

P总2

=

5

2

，
∵P=Fv，速度v相同，则：

P总1

P总2

=

2F1×4v

2F2×4v

=

8F1

8F2

=

G1+2G动

G2+2G动

=

5

2

∴2G₁=5G₂+6G_动，-------⑤
将G₁=3G₂，代入⑤式得：
G₂=6G_动，
将G₂=6G_动 代入①式得：
G₂=

12

5

F₁=

12

5

×500N=1200N，
可得：
G₁=3G₂=3×1200N=3600N，
G_动=

1

6

G₂=

1

6

×1200N=200N；
（2）η=

W有用2

W总2

=

G2h

G2h+ 2G轮h

=

G2

G2+ 2G轮

=

1200N

1200N+2×200N

=75%
答：（1）第一个货箱的重力为3600N；
（2）提升第二个货箱整个装置的机械效率为75%．

点评：本题为力学综合题，考查了功的计算、功率的计算、机械效率的计算，能进行正确的受力分析找出各量的关系式是本题的关键．