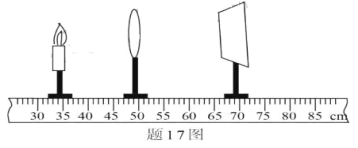
题目内容
【题目】如图所示,两根粗细均匀,横截面积相同但材料不同的金属棒焊接在一起,AB共长16cm,用第一种金属制成的部分AO=6cm,如果在两根金属棒焊接处O点支起它,恰好能在水平位置保持平衡.求: ![]()
①通过分析计算,判断这两根金属棒的质量是否相等?
②两种金属密度之比是多少?
(提示:规则形状的重力在其重心处)
【答案】解:①设AO段金属棒的重力为G1 , BO段金属棒的重力为G2; 因为AO长6cm,AB共长16cm,所以BO长10cm,
由于这两根金属棒粗细均匀,故它们的重心在几何中心,则G1的力臂是3cm,G2的力臂是5cm;
根据杠杆平衡条件可得:G1×3cm=G2×5cm﹣﹣﹣﹣﹣﹣①,
则可知:G1>G2 , 即m1>m2 .
②由①可得G1:G2=5:3,则金属棒AO与金属棒BO的质量之比为m1:m2=5:3;
由于这两根金属棒粗细均匀,所以它们的体积之比等于它们的长度之比,即V1:V2=3:5;
所以它们的密度之比是:ρ1:ρ2= ![]() :
: ![]() =
= ![]() :
: ![]() =25:9.
=25:9.
答:①这两根金属棒的质量不相等,AO段金属棒质量大;
②两种金属密度之比是25:9
【解析】①有支点且两根金属棒平衡,所以这道题是一道杠杆平衡题.那么要判断两根金属棒的质量是否相等,就应该用杠杆平衡条件去分析. 这两根金属棒的重力分别是杠杆的动力和阻力,它们的重心在几何中心上,则力臂正好是它们各自长度的一半.知道了力臂关系,根据杠杆平衡条件即可知道它们的重力关系,从而就可以判断出它们的质量关系.②要求密度之比,可先求出它们各自的质量之比与体积之比,最后综合一下就可以得出密度之比.
【考点精析】解答此题的关键在于理解密度的计算的相关知识,掌握密度公式:ρ = m/v,以及对杠杆的平衡条件的理解,了解杠杆平衡:杠杆在动力和阻力的作用下静止或匀速转动时,称为杠杆平衡.杠杆平衡是力和力臂乘积的平衡,而不是力的平衡.杠杆平衡的条件:动力 ×动力臂 = 阻力 ×阻力臂即:F1 L1 = F2 L2可变形为 :F1 / F2 = L1 / L2.

【题目】为了探究滑动摩擦力大小跟哪些因素有关,小明同学在老师的指导下,做了一系列实验,以下是部分实验步骤(实验过程中,保持长木板水平): 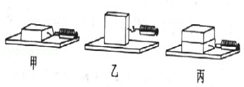
第1次:把木块平放在长木板上,用弹簧测力计水平拉木块作匀速直线运动(如图甲),读出弹簧测力计的示数,并记录表格中.
第2次:把木块侧放在长木板上,用同样的方法拉木块(如图乙),记下相应的示数.
第3次:把两块相同木块叠在一起平放在长木板上,再用同样的方法拉木块(如图丙),记下相应的示数:
(1)若已知木块质量为2kg,请你帮助小明填全表格内的数据;
实验次数 | 木块对木板的压力/N | 弹簧测力计的示数/N | 摩擦力/N |
1 | 20 | 4.0 | 4.0 |
2 | 4.0 | ||
3 | 8.0 |
(2)比较两次实验数据,可说明滑动摩擦力的大小与接触面积无关;
(3)比较第1、3两次实验数据,可以初步得出的结论是 .
(4)在实验过程中,小明应用了“控制变量法”,在第1次和第2次小明控制的物理量分别是和 . 也用到了“转换法”,小明根据条件把转换成 .
【题目】小明用图中所示的装置做“观察水的沸腾”实验. 
(1)如图乙所示,温度计的正确读数是℃.
(2)当水沸腾时,水中有一个气泡从A位置(体积为VA)上升至B位值(体积为VB),则VAVB(选填“>”、“等于”或“<”,下同),气泡在A、B两位置受到水的压强分别为PA和PB , 则pApB .
时间/min | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
温度/℃ | 90 | 92 | 94 | 96 | 98 | 98 | 98 | 98 | 98 |
(3)以上表格中的内容是小明记录的实验数据,则水的沸点是℃.
(4)实验完成后,烧杯内水的质量与实验前相比(选填“变大”、“不变”或“变小”).