Question

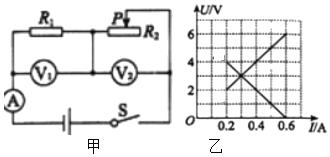
【题目】同学们在研究杠杆的平衡时，他们首先将装有某液体的圆柱形容器放在水平放置的电子台秤上（容器底面积S容＝0.02m2），台秤的示数为8kg。然后人站在水平地面上通过可绕O点转动的杠杆BC和轻绳将长方体A逐渐缓慢放入该液体中，直到A的上表面与液面相平，液体未溢出，此时杠杆在水平位置保持平衡，如图甲所示。已知：A的底面积为SA＝0.01m2，重力GA＝50N，人的重力G人＝518N，鞋与地面的总接触面积S鞋＝500cm2．当A从接触液面到恰好浸没时，A的下表面受到的液体压强随浸入液体的深度的变化图象如图乙所示。（g＝10N/kg，杠杆、轻绳质量均不计，轻绳始终竖直）求：

(1)长方体A未放入液体中时，容器对台秤的压强。

(2)容器中液体的密度。

(3)杠杆在水平位置平衡时，杠杆B端轻绳对长方体A的拉力。

(4)杠杆在水平位置平衡时，人双脚站立对地面的压强p＝1×104Pa，则OB与OC的长度之比为多少？

Answer 1

【答案】（1）4000Pa（2）1000kg/m3（3）30N（4）3：5

【解析】

(1)长方体A未放入液体中时，容器对台秤的压力为：

F＝G＝mg＝8kg×10N/kg＝80N，

容器对台秤的压强：

p==4000Pa；

(2)由图乙知长方体A的最大高度为20cm＝0.2m，此时下底面的压强为2000Pa，

根据p＝ρgh知，容器中液体的密度：

ρ＝＝＝1000kg/m3；

(3)长方体A的体积为：

VA＝SAh＝0.01m2×0.2m＝0.002m3，

A完全浸没时的浮力为：

F浮＝ρ液gV排＝1000kg/m3×10N/kg×0.002m3＝20N，

A浸没在液体中受重力、浮力和拉力，杠杆B端轻绳对长方体A的拉力：

FA＝GA﹣F浮＝50N﹣20N＝30N；

(4)杠杆在水平位置平衡时，根据p＝知，人双脚站立对地面的压力为：

F＝pS＝1×104Pa×500×10﹣4m2＝500N，

因为物体间力的作用是相互的，所以对面对人的支持力为500N，因为人受竖直向下的重力、竖直向上的支持力、竖直向上的拉力，所以人受到的拉力为:

F人＝G人﹣F支持＝518N﹣500N＝18N，

因为物体间力的作用是相互的，所以人对杠杆的拉力也为18N，根据杠杆的平衡条件F′人×LOC＝FA×LOB，OB与OC的长度之比为：

＝3：5。

答：(1)长方体A未放入液体中时，容器对台秤的压强为4000Pa。

(2)容器中液体的密度为1000kg/m3。

(3)杠杆在水平位置平衡时，杠杆B端轻绳对长方体A的拉力30N。

(4)杠杆在水平位置平衡时，人双脚站立对地面的压强p＝1×104Pa，则OB与OC的长度之比为3：5。