题目内容
用一个动滑轮把重为G=100N的物体提到h=9m的高处，人拉绳端的力F=60N问：（1）人做的总功是多少？
（2）人做的有用功是多少？
（3）人做的额外功是多少？
（4）动滑轮的机械效率是多大？
【答案】分析：由动滑轮的特点可以计算拉力移动的距离，由W=Fs计算出总功，由W有=Gh计算出有用功，则额外功等于总功减去有用功，机械效率等于有用功与总功的比值．
解答：解：（1）W=Fs=60N×9m×2=1080J．
（2）W有=Gh=100N×9m=900J．
（3）W额=W-W有=1080J-900J=180J．
（4）η=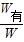
=
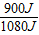=83.3%．
答：人做的总功是1080J，人做的有用功是900J，人做的额外功是180J，动滑轮的机械效率是83.3%．
点评：本题较简单，直接由公式可计算总功、有用功、额外功、机械效率．
解答：解：（1）W=Fs=60N×9m×2=1080J．
（2）W有=Gh=100N×9m=900J．
（3）W额=W-W有=1080J-900J=180J．
（4）η=
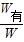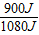==83.3%．答：人做的总功是1080J，人做的有用功是900J，人做的额外功是180J，动滑轮的机械效率是83.3%．
点评：本题较简单，直接由公式可计算总功、有用功、额外功、机械效率．
练习册系列答案
相关题目