题目内容
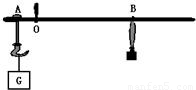
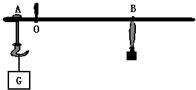 如图:杆秤砣的质量为0.5kg,秤钩悬挂处A与秤纽O间的距离为8cm,挂上重物后,秤砣移至距O点32cm的B处时,秤杆正好水平.求:
如图:杆秤砣的质量为0.5kg,秤钩悬挂处A与秤纽O间的距离为8cm,挂上重物后,秤砣移至距O点32cm的B处时,秤杆正好水平.求:(1)被称物体的质量.
(2)刻度为3千克的秤星与秤纽O点间的距离.(秤杆的重可忽略不计)
分析:(1)知道两边力臂大小,利用杠杆平衡条件和重力公式求被称物体的质量;
(2)知道被测物体的质量、OA的大小、秤砣质量,利用杠杆平衡条件求刻度为3千克的秤星与秤纽O点间的距离.
(2)知道被测物体的质量、OA的大小、秤砣质量,利用杠杆平衡条件求刻度为3千克的秤星与秤纽O点间的距离.
解答:解:(1)∵GA×OA=GB×OB,
即:mAg×OA=mBg×OB,
又∵OA=8cm,OB=32cm,
∴被称物体的质量:
mA=
=
=2kg;
(2)∵GA′×OA=GB×OB′,
即:mAg×OA=mBg×OB,
又∵OA=8cm,mA=3kg,mB=0.5kg,
OB′=
=
=48cm.
答:(1)被称物体的质量为2kg;
(2)刻度为3千克的秤星与秤纽O点间的距离为48cm.
即:mAg×OA=mBg×OB,
又∵OA=8cm,OB=32cm,
∴被称物体的质量:
mA=
| mB×OB |
| OA |
| 0.5kg×32cm |
| 8cm |
(2)∵GA′×OA=GB×OB′,
即:mAg×OA=mBg×OB,
又∵OA=8cm,mA=3kg,mB=0.5kg,
OB′=
| mA×OA |
| mB |
| 3kg×8cm |
| 0.5kg |
答:(1)被称物体的质量为2kg;
(2)刻度为3千克的秤星与秤纽O点间的距离为48cm.
点评:本题考查了杠杆平衡条件的应用,能确定两种情况下两边力和力臂的大小是本题的关键.

练习册系列答案
相关题目
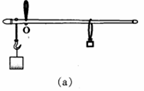
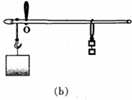
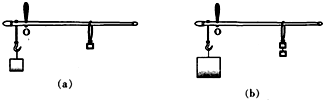 图(a)所示是一把杆秤的示意图,O是秤杆的悬点,使用该秤最多能称量5千克的重物.小王用一个相同的秤砣系在原来的秤砣下面,采用“双秤砣法”去称量7千克的重物时,秤上的示数为3千克,如图(b)所示.
图(a)所示是一把杆秤的示意图,O是秤杆的悬点,使用该秤最多能称量5千克的重物.小王用一个相同的秤砣系在原来的秤砣下面,采用“双秤砣法”去称量7千克的重物时,秤上的示数为3千克,如图(b)所示.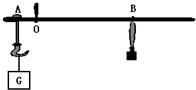 如图:杆秤砣的质量为0.5kg,秤钩悬挂处A与秤纽O间的距离为8cm,挂上重物后,秤砣移至距O点32cm的B处时,秤杆正好水平.求:
如图:杆秤砣的质量为0.5kg,秤钩悬挂处A与秤纽O间的距离为8cm,挂上重物后,秤砣移至距O点32cm的B处时,秤杆正好水平.求: